Сравнение алгоритмов сортировки

Подведем некоторые итоги. В данном разделе были рассмотрены наиболее известные (и лучшие) алгоритмы сортировки массивов. Эти алгоритмы разделяются на две группы: простые алгоритмы (сюда относятся «пузырек», выбор и вставки) и усовершенствованные ( алгоритмы Шелла, быстрой сортировки, пирамидальной сортировки и сортировки слиянием).

Общим недостатком простых алгоритмов является их слишком медленная работа на больших массивах данных. Это подтверждается как практикой использования, так и теоретической оценкой T(n) = O(n²). Усовершенствованные алгоритмы работают гораздо быстрее, причем на очень больших массивах различие может достигать многих тысяч раз.

Не следует делать из этого вывод, что всегда нужно применять только усовершенствованные алгоритмы. Для массивов малого размера различие в числе итераций незначительно, при этом даже возможно, что простые алгоритмы будут работать быстрее за счет более быстрого выполнения каждой итерации.

Где проходит граница между «маленькими» и «большими» массивами? Этот вопрос трудно решить теоретически, он должен решаться скорее на основе экспериментов, а также опыта и интуиции программиста.

Возникает также следующий вопрос. Есть ли основания останавливаться на пути усовершенствования алгоритмов сортировки, успокоившись на оценке T(n) = O(n·log(n))? Нельзя ли придумать алгоритм, имеющий существенно меньшую оценку?

Оказывается, что в классе алгоритмов, основанных на операциях сравнения ключей и перестановки записей, получить лучшую (в смысле O-большое) оценку нельзя. Чтобы доказать это, заметим, что любой исходный (несортированный) массив можно рассматривать как некоторую перестановку элементов сортированного массива. Для простоты будем считать, что все элементы массива различны, тогда эта перестановка единственна. Задача заключается в том, чтобы выполнить обратную перестановку, «привести в порядок» элементы. Очевидно, для правильного выполнения обратной перестановки нужно, как минимум, знать, какая именно из всех возможных перестановок n элементов имеет место в случае данного массива. Как известно, число таких перестановок равно n! (факториалу от n). Поставим вопрос: какое минимальное число сравнений ключей следует выполнить, чтобы гарантированно определить, какая из n! перестановок имеет место? Одно сравнение на «больше/меньше» позволяет, в лучшем случае, разбить множество перестановок на две равные половины. Для того чтобы при помощи таких разбиений наверняка выделить единственную перестановку, придется выполнить не менее, чем log₂(n!) сравнений. Из математики известно, что при больших n значение факториала можно приближенно определить по формуле Стирлинга:

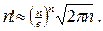
Отсюда

Как обычно, при переходе к оценке «в смысле O-большое» от формулы оставлен только главный член.

Полученная оценка показывает, что ни один алгоритм не позволит для числа сравнений получить лучшую оценку, чем O(n·log(n)). С учетом присваиваний оценка тем более не может улучшиться. Таким образом, дальнейшие исследования могут, конечно, привести к разработке лучших алгоритмов сортировки, но только в рамках оценки
T_max(n) = O(n·log(n)).

А что же тогда означает сделанная выше оговорка относительно «класса алгоритмов, основанных на операциях сравнения ключей и перестановки записей»? Возможны ли какие-то иные алгоритмы сортировки? Эти вопросы будут рассмотрены ниже, в разделах 5 и 6.

Вопросы и упражнения

1. Сколько сравнений выполняется при сортировке массива из n элементов по алгоритму пузырька?

2. При каком условии алгоритм пузырька может завершить сортировку массива за n–2 прохода? за n–3 прохода? На сколько операций сравнения меньше будет выполнено в этих случаях?

3. Предположим, что в алгоритме вставок значение переменной r сравнивается со значениями элементов массива не в обратном порядке (a_k, a_k–1, a_k–2 …, a₁), а в прямом (a₁, a₂, a₃ …, a_k). Повлияет ли это на правильность и эффективность алгоритма? Какой из двух вариантов больше подходит для сортировки Шелла?

4. Объясните, почему в нерекурсивном варианте QuickSort при занесении в стек более длинных отрезков глубина стека оказывается меньше, чем при занесении более коротких.

5. Объясните, почему в рекурсивном варианте QuickSort глубина используемого стека оказывается значительно больше, чем в нерекурсивном.

6. Запрограммируйте смешанный вариант QuickSort, в котором разделение массива и сортировка меньшего из получившихся отрезков выполняется в цикле, а для сортировки большего отрезка используется рекурсивный вызов (при этом нет необходимости явно использовать переменную-стек).

7. Какая глубина стека может потребоваться для реализации QuickSort, описанной в предыдущем упражнении?

8. Алгоритм сортировки называется устойчивым, если элементы массива, имеющие одно и то же значение ключа, сохраняют после сортировки свое взаимное положение. Какие из рассмотренных в разделе алгоритмов являются устойчивыми?

9. Дан массив чисел A = (10, 50, 30, 32, 11, 40, 20, 5, 16, 37, 12, 1). Выполнить сортировку массива по алгоритму ShellSort, используя значения h = 7, 3, 1. Показать состояние массива после каждого прохода.

10. Дан массив чисел A = (20, 13, 5, 25, 16, 18, 40, 32, 21, 11, 1, 30). Выполнить сортировку массива по алгоритму QuickSort. В качестве разделяющего выбирать первый элемент отрезка. Показать состояние массива после каждой операции разделения.

11. Дан массив чисел A = (35, 8, 24, 12, 42, 15, 31, 40, 14, 50). Выполнить преобразование массива в пирамиду (1-я фаза алгоритма HeapSort) и два первых прохода второй фазы алгоритма. Показать состояние массива после каждой операции просеивания.