Анализ правильности алгоритмов
На практике часто приходится встречаться с программами, содержащими ошибки. Например, в самой последней операционной системе Windows специалистами обнаружено много ошибок, которые время от времени выявляются на ЭВМ.
Программасодержит ошибки, если ее выполнение на ЭВМ приводит к получению сбоев, отказов или неправильных результатов. Программу в таком состоянии нельзя использовать для решения практических задач.
Проявления ошибок:
Программа
¯
данные ® ЭВМ ® { отказ | сбой | ошибка }
Отказ - это ситуация, когда выполнение программы прекращается вообще. Программы, содержащие такого рода ошибки считаются неработоспособными, и от их использования следует отказываться.
Сбой - это потеря части данных либо получение непредусмотренных данных. Такого рода ошибки говорят о их частичной неработоспособности программ либо об их недостаточной надежности.
Результат неправильный, если он не соответствует требованиям, предъявляемым к работе программ. Программы, содержащие такие ошибки, считаются работоспособными, но их применение может приводить к получению ошибочных результатов.
Оценка программ:
Задача
 |  |
 исходное требуемое
исходное требуемое
данные ® программа ® результаты
О правильности программнельзя утверждать ничего если неизвестны предъявляемые к ним требования. Только при наличии строгих, четких спецификаций можно судить о правильности работы программ.
В качестве примера рассмотрим решение квадратного уравнения:
х2 + 3×х + 2 = 0.
Исходные данные - коэффициенты – а = 1, b = 3, с = 2. Требуемые результаты - пара чисел х1 и x2, являющихся корнями уравнения. Посмотрим, будут ли корнями уравнения пары чисел:
а) х1 = 2, x2 = 3;б) x1 = -2, x2 = -3.
Решением уравнений являются числа, подстановка которых превращает уравнение в тождество. В первом случае подстановка чисел х1 = 2, х2 = 3 в уравнение дает:
22 + 3×2 + 2 = 12 ¹ 0 - неправильно,
32 +3×3+2 = 20 ¹ 0 - неправильно.
Следовательно, числа х1 = 2, х2 = 3 не являются правильными результатами.
Подстановка в уравнение чисел х1 = -2, х2 = -3:
(-2)2 + 3×(-2) +2 = 0- правильно;
(-3)2 + 3×(-3) +2 = 0- правильно.
Следовательно, числа х1 = -2, х2= -3 являются правильными результатами.
Приведем формальную постановку задачи решения квадратных уравнений.
Постановка задачи
Решение квадратного уравнения
а×х2 + b×x + с = 0.
Дано: a, b, с - коэффициенты.
Треб.: х1, х2 - корни.
Где: а×х12 + b×х1 + с = 0.
а×х22 + b×х2 + с =0.
При: а ¹ 0.
Наличие точной постановки задач позволяет говорить о правильности не только конечных результатов, но и различных способов и методов их решения.
Способ правильный, если он дает правильные результаты. Способ неправильный, если он дает неправильные результаты или не дает результатов вообще.
Метод неправильный, если существуют допустимые данные, для которых он дает неправильные результаты либо не дает результатов вообще.
Метод правильный, если он дает правильные результаты для любой задачи данного класса. Использование правильных методов служит основой для составления алгоритмов и программ, не содержащих ошибок.
В рассматриваемом примере решения квадратных уравнений общим методом является вычисление корней с помощью дискриминанта.
Метод решения
 x1 = (-b +
x1 = (-b + 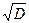 )/(2×а),
)/(2×а),
x2 = (-b - 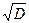 )/(2×a),
)/(2×a),
где
{ D = b2 - 4×а×с.
Правильность общих методов проверяется подстановкой расчетных формул в исходное уравнение. Получение тождеств в результате подстановок говорит о правильности выбранных расчетных формул.
Для первого корня х1 = (-b + 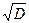 )/(2×a) подстановка и тождественные преобразования формул дадут:
)/(2×a) подстановка и тождественные преобразования формул дадут:
а×х12 + b×х1 + с = а×[(-b + 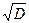 )/(2×а)]2 + b× (-b +
)/(2×а)]2 + b× (-b + 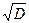 )/(2×a) + с =
)/(2×a) + с =
= (-b + 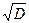 )2/(4×а) + b× (-b +
)2/(4×а) + b× (-b + 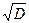 )/(2×a) + с = (b +
)/(2×a) + с = (b + 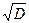 ) × (-b +
) × (-b + 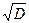 )/(4×а) + с =
)/(4×а) + с =
= (-b2 + D)/(4×a) + с = (-b2 + b2 - 4×а×с)/(4×а) + с = -4×а×с/(4×а) + с = 0.
Аналогичные результаты получаются и при подстановке формулы второго корня
х2 = (-b - 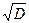 )/(2×a). После выполнения аналогичных преобразований будет получено такое же тождество. И на основании этих проверок можно сделать заключение, что рассмотренный метод дает правильные результаты для любык допустимых данных.
)/(2×a). После выполнения аналогичных преобразований будет получено такое же тождество. И на основании этих проверок можно сделать заключение, что рассмотренный метод дает правильные результаты для любык допустимых данных.
Однако саму постановку задачи необходимо дополнить условием: b2 - 4×а×с ³ 0. При нарушении этого условия не только уравнение не имеет решений, но и метод решения также не дает результатов из-за необходимости вычисления корней от отрицательного дискриминанта: D < 0.
В силу выбранного метода решения и принятой постановки алгоритм решения квадратных уравнений приобретает следующий вид:
алг «квадратное уравнение» Результаты вычислений
Нач
 если а ¹ О топри а ¹ 0
если а ¹ О топри а ¹ 0
D: = b*b - 4*а*с D = b2 - 4×а×с
 если D > = 0 то при D >= 0
если D > = 0 то при D >= 0
х1: = (-b +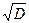 )/(2*a) х1 = (-b +
)/(2*a) х1 = (-b + 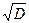 )/(2×a)
)/(2×a)
х2: = (-b - 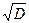 )/(2*a) х2 = (-b -
)/(2*a) х2 = (-b - 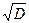 )/(2×a)
)/(2×a)
Все
 инеc а = 0 то при а = 0
инеc а = 0 то при а = 0
 если b ¹ 0при b ¹ 0
если b ¹ 0при b ¹ 0
х 1: = -c/b xl = -c/b
Все
Кон
Результаты выполнения алгоритма приведены справа. Можно заметить, что результаты выполнения совпадают с описанием выбранного метода решения с помощью дискриминанта. Это позволяет утверждать, что алгоритм - правильный.
Алгоритмсодержит ошибки, если можно указать допустимые исходные данные, при которых либо будут получены неправильные результаты, либо результаты не будут получены вовсе. Использование алгоритмов, содержащих ошибки, приводит к созданию программ, также содержащих ошибки.
Алгоритм считаетсяправильным, если он дает правильные результаты для любых допустимых исходных данных. Правильность алгоритмов решения прикладных задач и наличие в них ошибок можно проверять двумя основными способами.
Первый способ - проверка основных этапов построения алгоритма:
задача ® постановка ® метод ® алгоритм
Второй способ - анализ результатов выполнения алгоритмов и их сравнение с выбранными методами решения и постановкой задачи:
Дата добавления: 2016-04-06; просмотров: 997;
