Задача постановка метод алгоритм
Приведем пример построения алгоритма с одновременным анализом его правильности.
Задача: Определить периметр треугольника, заданного на плоскости координатами вершин.
XС,УС

XА,УА Xв,Ув
Постановка задачи
Определение периметра треугольника, заданного на плоскости.
 Дано: А = (ХА, УА)
Дано: А = (ХА, УА)
В = (ХВ, УВ) - координаты вершин треугольника
С = (XС,УС)
Треб.: Р - периметр
Метод решения
 Р = LАВ +LВС+LСА
Р = LАВ +LВС+LСА
LАВ = 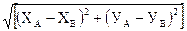
LВС = 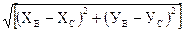
LСА = 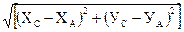
Где: Р = L(A,B) + L(B,C) + L(C,A);
здесь L[(x,y),(u,v)] = 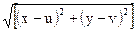 .
.
Приведем алгоритм, полученный из описания метода упорядочением операций вычисления длин сторон треугольника с завершающим вычислением периметра. Результаты выполнения алгоритма приведены справа.
алг «периметр треугольника»
Нач
LAB: = 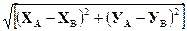
LBC : = 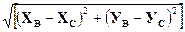
LCA : = 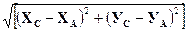
Р := LAB + LBC + LCA
Кон
 Результаты
Результаты
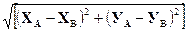
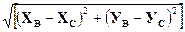
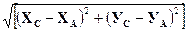
Р = LAB + LBC + LCA
Сравнение результатов выполнения алгоритма с описанием метода решения показывает, что это одна и та же система формул, что подтверждает правильность алгоритма.
Систематические методы анализа правильности алгоритмов и программ опираются на сопоставление тех же самых описаний, которые используются при их систематическом составлении.
Анализ правильности:
Задача способ
¯ ¯
Постановка методы
¯ ¯
Сценарий алгоритмы
¯ ¯
ЭВМ ® программа
Основные типы алгоритмических ошибок в программах:
· ошибки в выбранных методах решения;
· ошибки в постановке решаемых задач;
· дефекты в сценариях диалога с ЭВМ;
· ошибки организации ввода данных;
· неправильная реализация методов решения.
Исчерпывающий анализ правильности алгоритмов и устранение из программ ошибок всех перечисленных типов возможны только при наличии соответствующих спецификаций: постановок задач, описаний методов решения и спецификаций ввода-вывода данных.
Будем считать, чтопрограмма правильная, если она дает правильные результаты для любых допустимых исходных данных. Такого рода программы вполне можно использовать для решения прикладных задач.
Программа считаетсянадежной, если она не дает сбоев и отказов ни при каких исходных данных. Надежность - обязательное условие для всех программ, которые используются людьми для решения практических задач на ЭВМ.
В качестве иллюстрации приведем пример систематического составления алгоритма и программы задачи определения суммарного веса учеников по данным из таблицы:
Фамилия рост вес
| Иванов | ||
| Петрова | ||
| Сидоров |
Рассмотрим постановку задачи и метод вычисления суммарного веса.
Постановка задачи
Определение суммарного веса.
Дано:Метод вычисления
(D1,.., DN) - данные об учениках, S0 = 0
 где D = [Fam,R,V] - состав данных, Sk = Sk-1 + vk
где D = [Fam,R,V] - состав данных, Sk = Sk-1 + vk
Fam - фамилия, R - рост, V - вес. [k = (1 ... N)]
Треб.: Vsum - суммарный вес. Vsum = SN
Vsum = v1 + v2 + ... + vN
При: N > 0.
Правильность метода вычислений можно доказать по индукции. Рассмотрим результаты вычислений на 1-м, 2-м и k-м шагах. Отметим, что начальное значение S0 = 0.
На первом шаге при k = 1 результат вычисления
S1 = S0 +v1 = v1
На следующем втором шаге при k = 2 результат
S2 = S1 + v2 = v1 + v2.
На третьем шаге при k = 3 результат
S3= S2 + v3 = v1 + v2 + v3.
В общем случае можно предположить, что к k-му шагу результат вычисления
Sk-1=v1+...+vk-1.
Тогда результат вычислений после k-го шага (исходя из описания метода)
Sk = Sk-1 +vk = v1 + … + vk-1 + vk.
В силу принципа математической индукции утверждение верно для всех k = 1, 2,.... N. Следовательно, на последнем шаге при k = N конечный результат:
SN = v1 + ... + vN.
Что и требовалось. Следовательно, метод правильный.
Приведем сценарий диалога решения поставленной задачи на ЭВМ. Для представления данных в программе примем последовательность операторов data.
Сценарий Представление данных

Данные об учениках
фамилия вес рост


 dano:'данные учеников
dano:'данные учеников
<Fam1> <V1> <R1> data «Иванов», 185, 85
… … … data «Петрова», 165, 65
<FamN> <VN> <RN> data «Сидоров», 170, 80
 data «», 0, 0
data «», 0, 0
суммарный вес = <Vsum>
Алгоритм обработки данных и программа, соответствующие выбранному сценарию и методу вычисления:
АлгоритмПрограмма
алг «суммарный вес» ' суммарный вес
нач cls
вывод («Данные об учениках») ? «Данные об учениках»
вывод («фамилия вес рост») ? «фамилия вес рост»
s := 0 s = 0
цикл do
чтение famS, r, v read fam$, r, v
при fam$=«» выход if fam$=«» then exit do
вывод (fam$, v, r) ? fam$; v; r
s := s + v s = s + v
кцикл loop
vsum = s vsum = s
вывод («суммарный вec=»,vsum) ? «суммарный вес=»; vsum
кон end
Правильность приведенного алгоритма можно увидеть из описания результатов его выполнения.
АлгоритмРезультаты выполнения
алг «суммарный вес» на экране и в памяти ЭВМ
Нач
вывод («Данные об учениках») Данные об учениках
вывод («фамилия вес рост») фамилия вес рост
 s: = 0s0 = 0
s: = 0s0 = 0
Цикл
чтение fam$, r, v
при fam$=«» выход
вывод (fam$, v, r)<famk> <vk> <rk>
s: = s + v sk = sk-1 + vk
кцикл[k = (1...n)]
vsum = svsum = sn
вывод («суммарный вec=»,vsum) суммарный вес= <vsum>
Кон
Сопоставление описания результатов выполнения с описаниями сценария и выбранного метода говорит об их полном соответствии. Следовательно, составленные алгоритм и программа правильные.
В о п р о с ы
1. Когда программы содержат ошибки?
2. Что такое правильный способ решения?
3. Когда способ решения неправильный?
4. Что такое правильный метод решения?
5. Когда метод решения неправильный?
6. Что такое правильный алгоритм?
7. Когда алгоритм содержит ошибки?
8. Каковы основные типы ошибок в программах?
З а д а ч и
1. Приведите постановку задачи, сценарий, алгоритм и программу решения линейного уравнения а×х + b = 0, с помощью формулы х = -b/а (при а ¹ 0).
2. Приведите постановку задачи, сценарий, алгоритм и программу решения квадратного уравнения а×х2 + b×x + с = 0 с помощью формулы дискриминанта.
3. Приведите постановку задачи, сценарий, алгоритм и программу решения системы из двух уравнений с двумя неизвестными:
 а×х + Ь×у = е,
а×х + Ь×у = е,
с×х + d×y = f.
Примените для этой задачи вычисление корней с помощью определителей:
 х = Dx/D,
х = Dx/D,
y = Dy/D.
Определители D, Dx и Dy вычисляются по формулам:
 D = a×d - b×c,
D = a×d - b×c,
Dx = e×d - f×b,
Dy = a×f - c×e.
4. Приведите постановку, сценарии, алгоритм и программу решения следующих задач:
а) определение площади треугольника по длине сторон а, Ь, с по формуле Герона:

 S =
S = 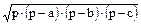 ,
,
р = (а + b + с)/2.
б) определение площади треугольника, заданного на плоскости координатами своих вершин: (х1, у1), (х2, у2), (х3, у3); для вычисления длин сторон треугольника воспользуйтесь формулой определения длин отрезков на плоскости, задаваемых координатами концов:
l = 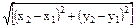
5. Приведите постановку, метод, сценарий, алгоритм и программу решения следующих задач:
а) определение времени встречи пешеходов, двигающихся навстречу друг другу;
б) определение времени, которое требуется пешеходу, чтобы догнать другого пешехода;
в) определение времени движения парохода по течению и против течения реки;
г) определение времени движения пешеходов навстречу друг другу, если один из них движется с замедлением;
д) определение времени падения тела с заданной высоты;
е) определение времени полета тела, брошенного вверх;
ж) определение расстояния, на которое улетит мяч, брошенный под углом к горизонту.
6. Дана прямоугольная матрица АNM - прямоугольная числовая таблица размера N ´ М. Приведите постановку, метод решения, сценарий, алгоритм и программу для решения следующих задач:
а) подсчет сумм элементов матрицы по столбцам,
б) подсчет сумм элементов матрицы по строкам,
в) нахождение минимального значения в каждом столбце,
г) нахождение минимального значения в каждой строке,
д) нахождение максимального значения в каждом столбце,
е) нахождение максимального значения в каждой строке,
ж) нахождение наибольшего из минимальных значений в столбцах,
з) нахождение наименьшего из максимальных значений в строках.
Дата добавления: 2016-04-06; просмотров: 994;
