II.8. Анализ и синтез САР

В практической работе при исследовании систем автоматического регулирования приходится иметь дело с двумя задачами.

В одних случаях при заданных системе, воздействиях на нее и известных начальных условиях требуется исследовать работу системы, найти процессы, в ней возникающие. Это задача анализа САР. В задачу анализа, таким образом, входит исследование устойчивости системы, исследование динамического и статического режимов работы САР.

В других случаях при заданных объекте управления и требованиях к системе управления этим объектом надо спроектировать такую САР, которая удовлетворяла бы поставленным требованиям. Это задача синтеза САР.

Обе задачи имеют много общего и в значительной степени связаны друг с другом. К настоящему времени задачи анализа и синтеза линейных САР в значительной степени решены. Что же касается решения этих задач для нелинейных САР, то оно пока далеко от завершения.

Большая часть этого учебного пособия (вплоть до главы V) будет посвящена задаче анализа систем автоматического регулирования, создания и использования инструментария этого анализа.

В практике автоматического регулирования часто возникает задача сравнения нескольких САР и выбора из них лучшей в том или ином смысле. Естественной представляется идея подать на все эти системы одинаковые пробные (тестовые) сигналы и по реакции на приложенные воздействия судить о качестве регулирования в каждой из них.

В теории автоматического регулирования применяются разнообразные тестовые сигналы. Нам понадобятся в дальнейшем три из них.

а). Единичный скачок (рис. II.28).

Понятно, что это сигнал является известной идеализацией реального скачка, т.к. для того, чтобы провести изменения сигнала от нулевого до любого значения мгновенно, устройство, производящее это изменение, должно обладать бесконечно большим коэффициентом усиления. Реальное устройство

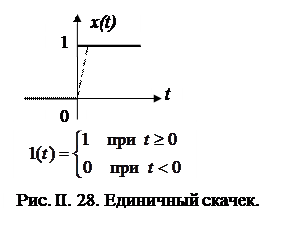
будет изменять сигнал за конечное время по некоторой зависимости, изображенной на рис. II.28 пунктирной линией, причем наклон этой линии зависит от коэффициента усиления устройства. Тем не менее, в дальнейшем мы будем употреблять идеализированное выражение этого сигнала.

б). Единичный импульс [дельта-функция Дирака d(t)] (рис. II.29)

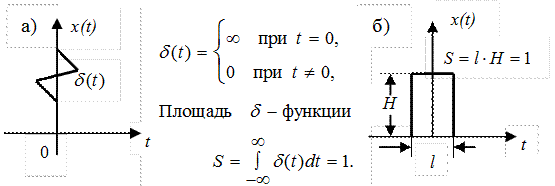
Рис. II.29 Единичный импульс.

Под единичным импульсом (d - функцией Дирака) понимают импульс бесконечно малой длительности бесконечно большой амплитуды с площадью

S = 1 (рис. II.29,а). Здесь значок “зигзаг”- условное обозначение d - функции. Понятно, что, как и в предыдущем случае, речь идет о некоторой идеализации, уяснить которую можно, обратившись к рис. II. 29,б. Пусть имеется импульс длительности l и амплитуды Н, площадь которого 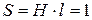. Будем, не изменяя площади, уменьшать длительность импульса l, увеличивая тем самым его амплитуду Н. В пределе как раз и получится d - функция.

в). Гармоничный сигнал .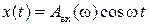

При анализе систем автоматического регулирования их можно исследовать во времени и частотной областях.