Функций динамических звеньев
Если при составлении уравнений звена принимаются во внимание все факторы, влияющие на динамику звена, то уравнения получаются, как правило, нелинейными. Иногда, как в примере П.II.1, уже на начальной стадии составления математического описания звена задают линейный характер процессов, протекающих в звене (например, обеспечивают работу звена на линейном участке характеристики, пренебрегают из-за очевидной малости гистерезисом, насыщением и т.п.). В этом случае полученные уравнения динамики звена уже получаются линейными и, следовательно, нет необходимости в их линеаризации. В иных случаях (как П.II.2) линеаризация необходима.
П.II.1. Найти передаточную функцию и дифференциальное уравнение пассивного четырехполюсника (рис. II.4)
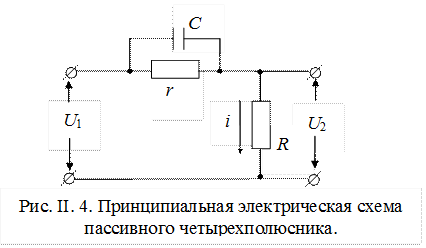
Решение.
По определению передаточная функция звена есть отношение Лапласовых изображений выходного сигнала к входному при нулевых начальных условиях. В нашем случае
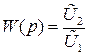
Выходное напряжение 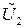 определяется, как падение напряжения на выходном сопротивлении R
определяется, как падение напряжения на выходном сопротивлении R
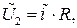
а ток 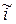 является результатом воздействия входного напряжения
является результатом воздействия входного напряжения 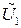 на полное сопротивление четырехполюсника
на полное сопротивление четырехполюсника
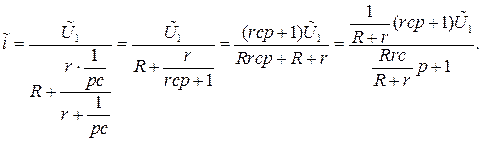
Тогда 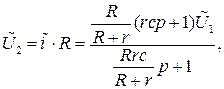
а передаточная функция искомого четырехполюсника
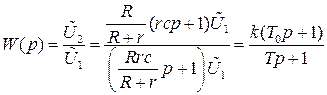
при обозначениях 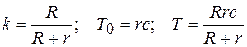 .
.
Из выражения для передаточной функции четырехполюсника получается его дифференциальное уравнение в Лапласовой области
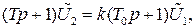
а во временной области будем иметь
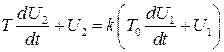 .
.
П.II.2. Получить передаточную функцию и дифференциальное уравнение двигателя постоянного тока с независимым возбуждением.
Решение.
Принципиальная электрическая схема рассматриваемого звена представлена на рис. II.5.
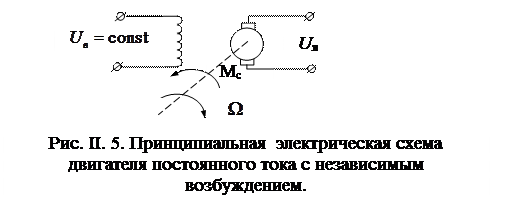
Работа этого элемента достаточно подробно излагается в курсе физики и электрических машин, поэтому здесь рассматриваться не будет.
Входным сигналом звена является якорное напряжение 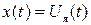 , а выходным - угловая скорость
, а выходным - угловая скорость 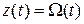 либо угол поворота вала двигателя
либо угол поворота вала двигателя 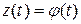 . Предполагается, что на валу двигателя имеется нагрузка, вызывающая момент сопротивления Мс.
. Предполагается, что на валу двигателя имеется нагрузка, вызывающая момент сопротивления Мс.

Таким образом, функциональная схема звена может быть представлена следующим образом (рис. II.6).
Хотя формально выражение, характеризующее основной закон функционирования данного звена, может быть представлено в виде
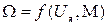 (II.4.1)
(II.4.1)
где М – вращающий (движущий) момент двигателя,
f – нелинейный дифференциальный оператор, однако действительный вид его неизвестен, ибо в документации на двигатель не задается конкретный вид оператора f. В паспорте на двигатель обычно даются его механические характеристики (рис. II.7).
Для базового режима 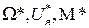 отметим точки А и В на механических характеристиках двигателя и запишем выражение, определяющее основной закон работы двигателя, имея, однако, в виду, что эта запись будет иметь чисто формальный характер, т.к. оператор f не задан
отметим точки А и В на механических характеристиках двигателя и запишем выражение, определяющее основной закон работы двигателя, имея, однако, в виду, что эта запись будет иметь чисто формальный характер, т.к. оператор f не задан
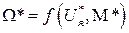 . (II.4.2)
. (II.4.2)
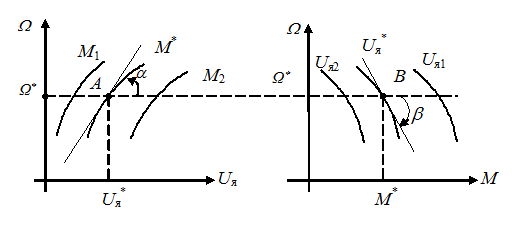
Рис. II. 7. Механические характеристики двигателя постоянного тока с независимым возбуждением.
Для фактического режима
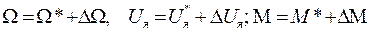
будем иметь
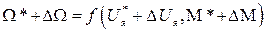 .
.
Поскольку отклонения 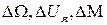 от базового режима невелики, разложим правую часть этого уравнения в ряд Тейлора и удержим только линейные члены разложения
от базового режима невелики, разложим правую часть этого уравнения в ряд Тейлора и удержим только линейные члены разложения
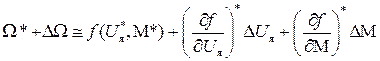 .
.
В силу (II.4.2) первые слагаемые левой и правой части этого соотношения равны, поэтому с учетом (II.4.1) это разложение примет вид
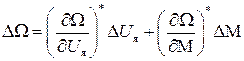 . (II.4.3)
. (II.4.3)
Этим самым мы провели линеаризацию, т.е. заменим нелинейное уравнение двигателя (II.4.1) линейным дифференциальным уравнением (II.4.3) с постоянными коэффициентами. Геометрически это означает, что кривые линии на рис. II.7 в районе базового режима А и В мы заменили прямыми. При этом надо иметь в виду, что если уравнение (II.4.1) носило формальный характер, т.к. оператор f не был задан, то уравнение (II.4.3) вполне конкретно, т.к. в точках базового режима коэффициенты 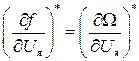 и
и 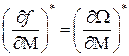 из механических характеристик (II.7) определяются однозначно. Понятно, что по своему физическому смыслу эти производные есть тангенсы углов наклона касательных к механическим характеристикам в точках базового режима
из механических характеристик (II.7) определяются однозначно. Понятно, что по своему физическому смыслу эти производные есть тангенсы углов наклона касательных к механическим характеристикам в точках базового режима
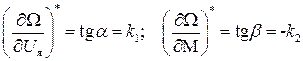
Здесь второе выражение взято со знаком минус, т.к. угол a отсчитывается против часовой стрелки, а угол b - по часовой. С учетом этих обозначений выражение (II.4.3) примет вид
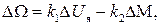
откуда найдем
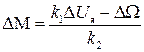 . (II.4.4)
. (II.4.4)
Запишем уравнение моментов на валу двигателя
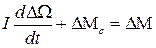 ,
,
где I – момент инерции подвижных масс, приведенных к выходному валу двигателя.
Подставим в это уравнение DМ из (II.4.4)
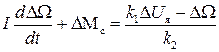 .
.
Отсюда получим, перейдя в область преобразования Лапласа
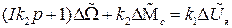 .
.
Пусть нагрузка на валу двигателя постоянна, тогда 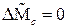 . С учетом обозначения
. С учетом обозначения
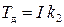
получим в Лапласовой форме дифференциальное уравнение двигателя постоянного тока (особо подчеркнем здесь, что пока мы рассматриваем случай, когда выходной величиной двигателя является его угловая скорость вращения)
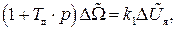
откуда легко находится передаточная функция двигателя постоянного тока
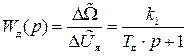
Выше уже говорилось, что значок D в математических выражениях опускается
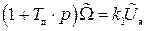 . (II.4.5)
. (II.4.5)
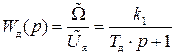 , (II.4.6)
, (II.4.6)
т.е. по умолчанию предполагается, что линеаризация уже проведена, и под переменными 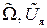 надо понимать их отклонения от базовых значений.
надо понимать их отклонения от базовых значений.
Перехода в (II.4.5) в область вещественного переменного t, получим дифференциальное уравнение двигателя постоянного тока
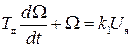 .
.
Поскольку 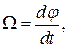 или
или 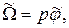 то с учетом этого формула (II.4.6) примет вид
то с учетом этого формула (II.4.6) примет вид
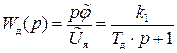 .
.
Отсюда передаточная функция двигателя постоянного тока, выходной координатой которого является угол поворота вала, примет вид
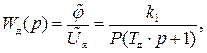 (II.4.7)
(II.4.7)
а соответствующее дифференциальное уравнение
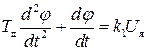 . (II.4.8)
. (II.4.8)
Приведем теперь без вывода передаточные функции часто встречающихся элементов САР.
П. II. 3. Линейный потенциометр

Здесь (на рис. II.8) обозначено
U – напряжение питания потенциометра,
m – перемещение ползунка потенциометра из начального положения (входной сигнал),
l – полная длина намотки потенциометра.
Um – напряжение снимаемое с движка потенциометра (выходной сигнал).
Легко понять, что
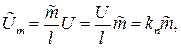
где 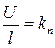 - коэффициент передачи (усиления) потенциометра, следовательно, передаточная функция потенциометра будет
- коэффициент передачи (усиления) потенциометра, следовательно, передаточная функция потенциометра будет
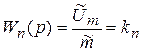 . (II.4.9)
. (II.4.9)
П. II. 4. Редуктор
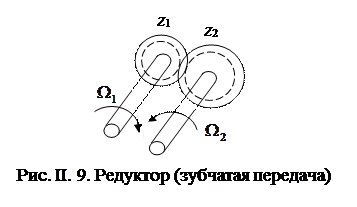
Редуктор предназначен для изменения угловой скорости вращения выходного вала и, в некоторых случаях, изменения направления вращения. На рис. II.9 представлен редуктор (зубчатая передача), состоящая из двух зубчатых колес с числом зубьев, соответственно, z1 и z2. Чаще редуктор имеет более сложную структуру и состоит из большего числа зубчатых колес.
Передаточным числом редуктора i называется отношение между угловыми скоростями ведущего и ведомого валов или отношений числа зубьев ведомого и ведущего валов
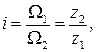
где 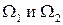 - угловые скорости, соответственно, ведущего и ведомого валов (входной и выходной сигналы). Из этого выражения, переходя в Лапласову область, получим
- угловые скорости, соответственно, ведущего и ведомого валов (входной и выходной сигналы). Из этого выражения, переходя в Лапласову область, получим
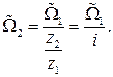
Положив коэффициент передачи редуктора 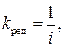 получим алгебраическое уравнение редуктора
получим алгебраическое уравнение редуктора
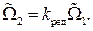
Тогда передаточная функция редуктора
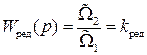 . (II.4.10)
. (II.4.10)
П. II. 5. Электронный усилитель

Электронный усилитель передназначен для усиления сигнала по напряжению. Обозначив через Uвк входное напряжение усилителя, а через Uвых – выходное, можно записать уравнение рассматриваемого звена
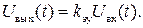
Передаточная функция усилителя
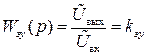 . (II.4.11)
. (II.4.11)
Здесь kэу – коэффициент усиления электронного усилителя.
П. II. 6. Тахогенератор постоянного тока
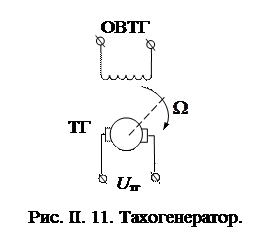
Тахогенератор постоянного тока применяется чаще всего в системах автоматического регулирования в качестве датчика угловой скорости вращения в различных измерительных системах. На рис. II. 11 изображено:
ТГ- тахогенератор постоянного тока,
ОВТГ – обмотка возбуждения тахогенератора,
W - угловая скорость вращения тахогенератора (и связанного с ним двигателя), - входной сигнал,
Uтг – напряжение тахогенератора (выходной сигнал).
Тахогенератор представляет собой машину постоянного тока. Его вал механически связан с валом двигателя, угловую скорость которого он (тахогенератор) предназначен измерять.
Уравнение тахогенератора может быть записано в следующем виде
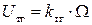 ,
,
где kтг – постоянный коэффициент, а передаточная функция
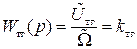 . (II.4.12)
. (II.4.12)
Так как 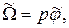 где
где 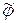 - угол поворота вала, то можно записать
- угол поворота вала, то можно записать
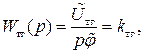
или
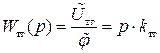 ,
,
т.е. если записать передаточную функцию тахогенератора постоянного тока относительно угла поворота вала двигателя, то тахогенератор может быть представлен в виде идеального дифференцирующего звена (см. III.1.4).
П. II. 7. Генератор постоянного тока с независимым возбуждением

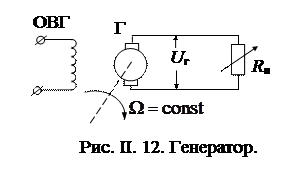
Генератор постоянного тока предназначен для усиления сигнала по току и по мощности. На рис. II.12 обозначено:
Г – генератор постоянного тока,
ОВГ – обмотка возбуждения генератора,
Rн – нагрузка генератора.
Входным сигналом звена является напряжение возбуждения Uв выходным – напряжение на зажимах генератора Uг.
Генератор приводится во вращение от вспомогательного двигателя (на рис. не показан) с угловой скоростью W = const.
В [3] показано, что дифференциальное уравнение генератора может быть представлено в виде
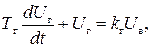 (II.4.13)
(II.4.13)
где kг – коэффициент усиления генератора,
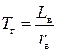 - постоянная времени генератора,
- постоянная времени генератора,
LB – индуктивное сопротивление ОВГ,
rB – активное сопротивление ОВГ.
Переходя в Лапласову область из (II.4.13) получим передаточную функцию генератора
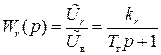 (II.4.14)
(II.4.14)
П. II. 8. Электромашинный усилитель с поперечным полем
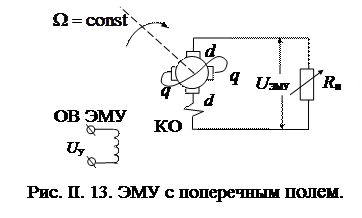
В автоматизированных приводах прокатных станах, моторных машинах, копировально-фрезерных автоматах и других типах следящих приводов в качестве усилителей мощности широкое применение получили электромашинные усилители (ЭМУ). Современные ЭМУ с поперечным полем имеют коэффициент усиления по мощности 1000 ¸500000. Отечественная промышленность выпускает ЭМУ мощностью от 30 Вт до 100 кВт.
Схема ЭМУ с поперечным полем дана на рис. II.13. Здесь ЭМУ приводится во вращение от постороннего двигателя, не показанного на рисунке, с постоянной угловой скоростью W = const. Входной величиной является напряжение возбуждения Uу на обмотке возбуждения ОВ ЭМУ, выходной – напряжение на зажимах ЭМУ – UЭМУ. Буквами d-d обозначена продольная цепь ЭМУ, буквами q-q – поперечная. Под Rн понимается нагрузка ЭМУ. Дополнительная обмотка КО – компенсационная и предназначенная для уничтожения реакции якоря.
Согласно [5] передаточная функция ЭМУ с поперечным полем дается выражением
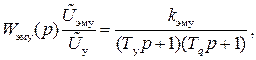 (II.4.15)
(II.4.15)
отсюда получим дифференциальное уравнение ЭМУ в операторной форме
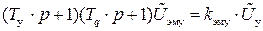
и во временной области
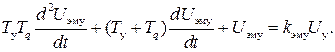 (II.4.16)
(II.4.16)
В уравнениях (II.4.15) и (II.4.16) приняты обозначения
КЭМУ – коэффициент усиления,
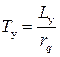 - постоянная времени цепи управления,
- постоянная времени цепи управления,
Ly – индуктивное сопротивление ОВ ЭМУ,
ry – активное сопротивление ОВ ЭМУ,
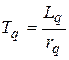 - постоянная времени поперечной цепи ЭМУ,
- постоянная времени поперечной цепи ЭМУ,
Lq – индуктивное сопротивление поперечной цепи ЭМУ,
rq – активное сопротивление поперечной цепи ЭМУ.
Дата добавления: 2016-04-14; просмотров: 2479;
