L – класс линейных функций.

L = {f(x₁, ...)| f = c₀Åc₁x₁Å...Åc_nx_n}; очевидно, L ¹ Æ, с другой стороны

L ¹ P₂, так как x₁&x₂ Ï L. Заметим, что тождественная функция принадлежит L и |L(n)| = 2ⁿ⁺¹. Покажем, что [L] Í L. Рассмотрим Ф = f(f₁, ..., f_m), где f, f₁, ..., f_n Î L. Тогда Ф = а₀ Å а₁(с₁₀ Å с₁₁х₁ Å...Å c_1nx_n1) Å a₂(c₂₀ Å c₂₁x₁ Å c₂₂x₂Å ...Å c_2nx_n2)Å...Å a_n(c_m0 Åc_m1x₁ Å ... Å c_mnx_nm) = в₀ Å в₁х₁ Å ...Å в_nх_n Þ ФÎL.

5) М – класс монотонных функций.

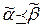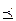
Определение. Набор = (a₁, ..., a_n) предшествует набору = (b₁, ..., b_n) и обозначается , если для 1£i£n a_i£b_i, например: = (0010), = (0110), тогда . Не любые два набора находятся в отношении предшествования, например, наборы (0110) и (1010) в таком отношении не находятся. Отношение предшествования ( 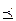) является отношением порядка на множестве наборов длины n, множество таких наборов будет частично упорядоченным множеством по отношению к операции.

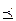
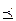Определение. Функция f(x₁, ..., x_n) называется монотонной, если для двух наборов и , таких что , выполняется f( ) f( ). Функции 0, 1, x, x₁&x₂, x₁ Ú x₂ Î M, x₁¯x₂, x₁ Å x₂, x₁ ~ x₂ Ï M.

Для числа монотонных функций, зависящих от n переменных, существуют оценки сверху и снизу, но точное число сосчитать не удается. Покажем, что М замкнутый класс. Рассмотрим функцию ФÎ[M], Ф = f(f₁, ..., f_m), где f, f₁, ..., f_mÎM, причем можем считать, что все они зависят от n переменных. Пусть набор 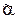= (a₁, ..., a_n), = (b₁, ..., b_n). Рассмотрим Ф(a₁, ..., a_n) = f(f₁(a₁, ..., a_n), …, f_m(a₁, ..., a_n)) и Ф(b₁, ..., b_n) = f(f₁(b₁, ..., b_n), ..., f_m(b₁, ..., b_n)). Здесь f₁(a) 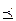f₁(b), ..., f_m(a)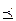 f_m(b), тогда набор (f₁(a), ..., f_m(a)) 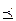(f₁(b), ..., f_m(b)), но тогда Ф(a) 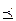Ф(b), так как fÎM, отсюда Ф = f(f₁, ..., ) – монотонная функция.

Определение. Функция f есть суперпозиция над M, если f реализуется некоторой формулой над M.

Лемма о немонотонной функции. Отрицание можно получить суперпозицией констант 0 и 1, тождественной функции и немонотонной функции.

Доказательство. Пусть f(x₁, ..., x_n) – немонотонная функция. Тогда существуют наборы 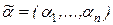и 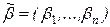, для которых 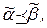но 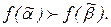Пусть i₁, …, i_k есть все те номера аргументов, для которых 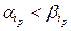, p=1, …, k. На всех остальных аргументных местах j имеем a_j = b_j. В выражении 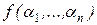заменим нули на местах i₁, …, i_k на x. В результате получим функцию g(x), для которой g(0) = f( 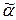) = 1 и g(1) = f( ) = 0. Функция g(x) является отрицанием.

Классы T₀, T₁, L, S, M пересекаются, но не совпадают, что видно из следующей таблицы, где «+» означает, что функция принадлежит данному классу и «-» – не принадлежит.

	T0	T1	L	S	M
x	+	+	+	+	+
	-	-	+	+	-
	+	-	+	-	+
	-	+	+	-	+
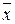
x1x2	+	+	-	-	+

A={x, 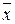, 0, 1, x₁x₂) не является полной системой функций так как всегда есть функции Î Р₂ не входящие в эти классы.

Задачи

1. Доказать, что пересечение любых двух замкнутых классов замкнуто.

2. Доказать, что объединение двух замкнутых классов не всегда замкнуто.