Представление функции в виде полинома Жегалкина

1. Представим любую функцию формулой над {x₁&x₂, 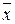} и сделаем замену 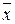=xÅ1. Этот способ удобен, если функция задана формулой.

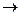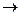Пример 2. (x₁ (x₂ x₃))(x₁ Ú x₂) x₃ = (x₁Ú x₂ Ú x₃)(x₁ Ú x₂) x₃ = (`x<sub>1</sub>x<sub>2</sub> Ú x<sub>1</sub>x<sub>3</sub> Ú x<sub>1</sub>x<sub>2</sub> Ú x<sub>2</sub> Ú x<sub>2</sub>x<sub>3</sub>)x<sub>3</sub> = (`x₁x₃ Ú x₂)x₃ = x₁x₃ x₂ x₃ = ((x₁x₃Å1)x₂Å1)x₃ = x₁x₂x₃Åx₂x₃Åx₃.

Надо помнить, что четное число одинаковых слагаемых в сумме по mod2 дает 0.

2. Метод неопределенных коэффициентов. Он удобен, если функция задана таблицей.

Пример 3. Запишем с неопределенными коэффициентами полином Жегалкина для функции трех переменных f(x₁, x₂, x₃) = (01101001) = а₀ Å а₁х₁Å Å а₂х₂ Å а₃х₃ Å b₁x₁x₂ Å b₂x₂x₃ Å b₃x₁x₃ Å cx₁x₂x₃. Затем находим коэффициенты, используя значения функции на всех наборах. На наборе (0, 0, 0) f(0, 0, 0) = 0, с другой стороны, подставив этот набор в полином, получим f(0, 0, 0) = а₀, отсюда а₀ = 0. f(0, 0, 1) = 1, подставив набор (0, 0, 1) в полином, получим: f(0, 0, 1) = а₀ Å а₃, т.к. а₀ = 0, отсюда а₃ = 1. Аналогично, f(0, 1, 0) = 1 = а₂, f(0, 1, 1) = 0 = а₂ Å а₃ Å b₂ = b₂ = 0; а₁ = 1; 0 = а₁ Å а₃ Å b₃ = b₃ = 0; 0 = а₁ Å а₂ Å b₁ = b₁ = 0; 1 = 1 Å 1 Å 1 Å c; c = 0; f(x₁, x₂, x₃) = x₁ Å x₂ Å x₃.

3. Многочлен Жегалкина можно получить также с помощью треугольника Паскаля по единицам его левой стороны по таблице следующим образом. Построим многочлен Жегалкина для функции f = (10011110). Верхняя сторона треугольника есть функция f. Любой другой элемент треугольника есть сумма по модулю для двух соседних элементов предыдущей строки. Левая сторона треугольника для функции f содержит шесть единиц. Многочлен Жегалкина будет содержать шесть слагаемых. Первая единица треугольника соответствует набору (000). Первое слагаемое многочлена есть 1. Третья снизу единица в левой стороне треугольника соответсвует набору (101). В качестве слагаемого многочлена берем x₁x₃. Аналогично для других единиц треугольника. Слева от наборов показаны слагаемые многочлена Жегалкина.

Тогда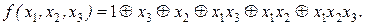

Теорема Жегалкина

Каждая функция из 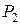может быть представлена в виде полинома Жегалкина единственным образом.

Здесь единственность понимается с точностью до порядка слагаемых в сумме и порядка сомножителей в конъюнкциях:

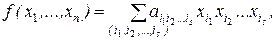
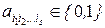, s = 0, 1, ..., n. Доказательство. Любая функция из Р₂ может быть представлена формулой над {x₁ & x₂, x₁Å x₂, 0, 1}, а эта формула после раскрытия всех скобок и приведения подобных членов дает полином Жегалкина. Докажем единственность представления. Рассмотрим функции f(x₁, ..., x_n) от n переменных. Мы знаем, что всего таких функций, т.е. их таблиц истинности , 2ⁿ. Подсчитаем число различных полиномов Жегалкина от n переменных, т.е. число вариаций вида: 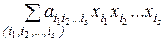. Число наборов 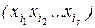равно числу всех подмножеств множества { x₁, ..., x_n }, сюда входит и пустое множество (если s = 0). Число подмножеств множества из n элементов равно 2ⁿ , а так как каждый набор входит с коэффициентом 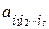, принимающим два значения: 0 или 1, то число всевозможных полиномов будет 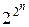. Так как каждому полиному соответствует единственная функция, число функций от n переменных равно числу полиномов, то каждой функции будет соответствовать единственный полином.

Определение.Функция f(x₁, ..., x_n), полином Жегалкина для которой имеет следующий линейный относительно переменных вид: f = а₀ Å а₁х₁ Å а₂х₂ Å ... Å а_nх_n, называется линейной.

Лемма о нелинейной функции. Суперпозицией нелинейной функции, отрицания и константы 1 можно получить конъюнкцию.

Доказательство. Пусть f(x₁, ..., x_n) – нелинейная функция. Тогда полином Жегалкина содержит для нее слагаемое, в котором присутствует произведение x_ix_j. Будем считать для простоты, что x₁x₂ в многочлене Жегалкина является этим произведением. Произведя группировку слагаемых, функцию f представим в виде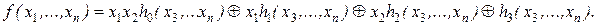

Функция h₀ не есть тождественный нуль, иначе в полиноме Жегалкина отсутствует слагаемое с произведением x₁x₂. Тогда существует набор (a₃, …, a_n) из 0 и 1, для которого h₀(a₃, …, a_n) = 1. Пусть h₁(a₃, …, a_n) = a, h₂(a₃, …, a_n) = b, h₃(a₃, …, a_n) = c. Тогда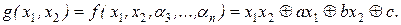

Построим функцию:

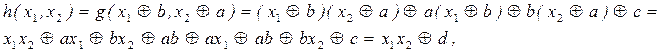где d = ab Å c. Если d = 0, то h(x₁, x₂) = x₁x₂. Если d = 1, то h(x₁, x₂) = x₁x₂ Å 1 и тогда 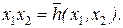Лемма доказана.

Функция f(x₁, ..., x_n) сохраняет константу a Î {0, 1}, если f(a, …, a) = a.

Пример 4. Функция xy сохраняет 0, сохраняет 1. Функция x®y сохраняет 1 и не сохраняет 0.