II. Статистические функции Маткада.
В Маткаде существуют целый набор встроенных функций для вычисления числовых характеристик случайной величины. К ним относятся:
1.mean (A) – возвращает среднее значение вектора А.
2.cvar(A,B) – возвращает корреляционный момент случайных векторов А и В.
3. stdev( A) – возвращает стандартное (среднеквадратическое) отклонение элементов вектора A.
4.corr(vx,vy) –возвращает коэффициент корреляции векторов vx vy.
6. hist (i, v)- функция построение гистограммы. Здесь i - вектор границ интервала, v- вектор случайных наблюдений. Ответ получаем в виде вектора размерностью вектора i, в котором помещено количество значений случайной величины, попавшей в каждый интервал и др. На рис.3 показано вычисление среднего арифметического и среднеквадратического ( стандартного) отклонения вектора случайных величин х..
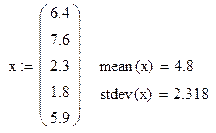
Рис.3 Вычисление среднего арифметического и с. к.о.
Задача 3.Провести решение и построение вышеприведенного графика .
Задача 4.вычислить корреляционный момент и коэффициент корреляции по заданным реализациям случайных величин Х , У и Z, W.
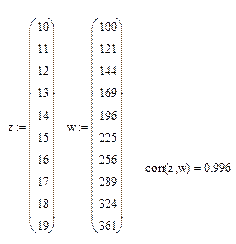
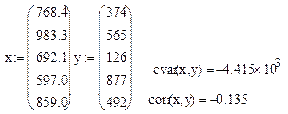
Рис.4.Вычисление корреляционного момента и коэффициента корреляции.
Примечание: случайная величина w является неслучайной функцией (квадратом) величины Z . Поэтому теоретически коэффициент корреляции должен был быть равен 1.
Задача 5. Известен курс двух валют: доллара США и монгольского тугрика. Спрашивается: зависит ли тугрик от доллара?
И курс доллара, и курс тугрика являются случайными величинами. Из предмета «Теория вероятностей» известно, что мерой статистической связи двух случайных величин является их коэффициент взаимной корреляции, определяемый по формуле:
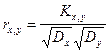 ,
,
где Kx,y -корреляционный момент двух случайных величин, а Dx ,Dy - дисперсии случайных величин.
Коэффициент корреляции может изменяться в пределах -1<= rx,y<=1. В таблице приведен курс доллара и тугрика за определенный период времени. Найти коэффициент корреляции.
Задача 6.По заданным реализациям случайной величины Х построить ее гистограмм
| Интервалы Наблюдений | -4-;3 | -3;-2 | -2;-1 | -1;0 | 0;1 | 1;2 | 2;3 | 3;4 |
| Число наблюдений в данном интервале | ||||||||
| Частота m/n | 0.012 | 0.05 | 0.144 | 0.266 | 0.240 | 0.176 | 0.092 | 0.02 |
му. Произведено 500 наблюдений. Результаты наблюдений сведены в статистический ряд:
Требуется построить гистограмму этого ряда. Гистограмма реализуется в Маткаде с помощью нескольких функций. Так как нам уже заданы частоты попадания случайной величины в каждый интервал, то мы построим ее следующим образом:
1. Сформируем векторы интервалов наблюдений v и частот f ( приведены для экономии места в транспонированной форме)
2. 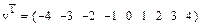
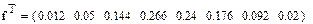
3. Используя функцию Histogram, найдем центры каждого интервала
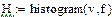
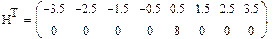
Матрица Н также приведена в транспонированной форме.
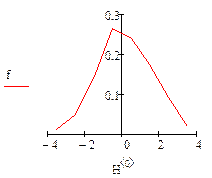 Построим плоский график, введя по оси абсцисс первый столбец матрицы Н, а по оси ординат – вектор f.
Построим плоский график, введя по оси абсцисс первый столбец матрицы Н, а по оси ординат – вектор f.
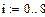
 Вызовем на панели форматирования (Formating Currently Selected X-Y Plot) окно Traces ( следы) и в столбце Тип выберем строку Solid Bar.Получим график гистограммы, показанной ниже.
Вызовем на панели форматирования (Formating Currently Selected X-Y Plot) окно Traces ( следы) и в столбце Тип выберем строку Solid Bar.Получим график гистограммы, показанной ниже.
Задача 7.Во многих случаях при статистических вычислениях требуется проводить выравнивание статистических рядов, т.е. сортировку их по возрастанию аргумента.
Для этого можно использовать функциюcsort.
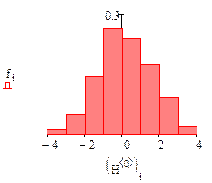
Пусть для значений аргумента Х, представленного вектором Х произведены наблюдения Y и Z, представленные векторами y и z.
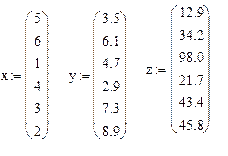
Для сортировки необходимо сформировать матрицу М, в которой первый столбец составляет вектор Х, второй - вектор У, третий - вектор Z.
Так как нам удобнее начинать отсчет с 1, введем ORIGIN=1
Дальнейшая последовательность действий понятна из рис.7 .
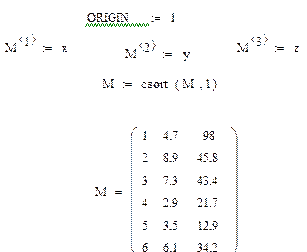
Рис. 7 Сортировка по Х.
Цифра 1 в функции CSORT означает, что сортировка производится по первому столбцу.
Дата добавления: 2016-04-11; просмотров: 3226;
