Численное решение нелинейных алгебраических уравнений.

В Маткаде корни алгебраических уравнений и систем определяются с помощью следующих встроенных функций:

1). Функция root (expr, var) вычисляет действительное значение переменной var, при котором выражение expr равно нулю, т.е. она вычисляет один действительный корень уравнения. При этом необходимо задать его начальное приближение. Ниже приведен пример использования этой функции для нахождения действительного корня уравнения

x² +2x+1 = 0.

Само уравнение не набирается!

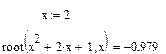
Рис.4. Нахождение одного корня полинома.

2) Функция polyroots (v) позволяет вычислять все корни полинома.

Например, для решения уравнения

8х² +2х +3 =0

набираем или считываем из таблицы функций (кнопка f(x)) функцию polyroots и в скобках заполняем вектор, вставляя коэффициенты уравнения. Нажимаем клавишу = и получаем ответ:

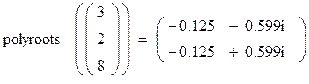
Рис.5. Вычисление корней с помощью функции Polyroots.

Следует обратить внимание, на то, что первый элемент вектора соответствует ко­эффициенту уравнения при свободном члене.

Задача 5.Вычислить в Маткаде корни приведенного выше уравнения.

Задача 6.Вычислить все корни многочленов

А) 5x⁵+6x³+8x²+2x=0

Б) 5x⁴+8x³+3x²+9x+8=0.

В).4x⁴+8x-3=0

Решение алгебраических уравнений в аналитической (символьной) форме.

Маткад предоставляет возможность решения алгебраических уравнений в символьной

( аналитической) форме. Преимуществом символьного решения является возможность решения уравнений с буквенными значениями коэффициентов. Правда, более или менее сложные уравнения символьно в Маткаде не решаются, поэтому приходится обращаться к численным методам.