Аппроксимация характеристик нелинейных элементов

Часто необходимо иметь аналитические выражения для вольт - амперных характеристик нелинейных элементов. Эти выражения могут лишь приближенно представлять ВАХ, поскольку физические закономерности, которым подчиняются зависимости между напряжениями и токами в нелинейных приборах, не выражаются аналитически.

Задача приближенного аналитического представления функции, заданной графически или таблицей значений, в заданных пределах изменения ее аргумента (независимой переменной) называется аппроксимацией. При этом во-первых, делается выбор аппроксимирующей функции, т. е. функции, с помощью которой приближенно представляется заданная зависимость, и, во-вторых, выбор критерия оценки «близости» этой зависимости и аппроксимирующей ее функции.

В качестве аппроксимирующих функций используются, чаще всего, алгебраические полиномы, некоторые дробные рациональные, экспоненциальные и трансцендентные функции или совокупность линейных функций (отрезков прямых линий).

Будем считать, что ВАХ нелинейного элемента i = fun(u) задана графически, т. е. определена в каждой точке интервала U_min ≤ и ≤ U_max, и представляет собой однозначную непрерывную функцию переменной и. Тогда задача аналитического представления вольт-амперной характеристики может рассматриваться как задача аппроксимации заданной функции ξ(х) выбранной аппроксимирующей функцией f(x).

О близости аппроксимирующей f(x)и аппроксимируемой ξ(х)функций или, иными словами, о погрешности аппроксимации, обычно судят по наибольшему абсолютному значению разности между этими функциями в интервале аппроксимации а ≤ х ≤ b, т. е. по величине

Δ= max‌‌│ f(x)- ξ(x)│

Часто критерием близости выбирается среднее квадратичное значение разности между указанными функциями в интервале аппроксимации.

Иногда под близостью двух функций f(x)и ξ(x) понимают совпадение в заданной точке

x = Хо самих функций и п + 1 их производных.

Наиболее распространенным способом приближения аналитической функции к заданной является интерполяция (метод выбранных точек), когда добиваются совпадения функций f(x)и ξ(x) в выбранных точках (узлах интерполяции) X_k, k = 0, 1, 2, ..., п.

Погрешность аппроксимации может быть достигнута тем меньшей, чем больше число варьируемых параметров входит в аппроксимирующую функцию, т. е., например, чем выше степень аппроксимирующего полинома или чем больше число отрезков прямых содержит аппроксимирующая линейно-ломаная функция. Одновременно с этим, естественно, растет объем вычислений, как при решении задачи аппроксимации, так и при последующем анализе нелинейной цепи. Простота этого анализа наряду с особенностями аппроксимируемой функции в пределах интервала аппроксимации служит одним из важнейших критериев при выборе типа аппроксимирующей функции.

В задачах аппроксимации вольт-амперных характеристик электронных и полупроводниковых приборов стремиться к высокой точности их воспроизведения, как правило, нет необходимости ввиду значительного разброса характеристик приборов от образца к образцу и существенного влияния на них дестабилизирующих факторов, например, температуры в полупроводниковых приборах. В большинстве случаев достаточно «правильно» воспроизвести общий усредненный характер зависимости i = f(u)в пределах ее рабочего интервала. Для того чтобы была возможность аналитически рассчитывать цепи с нелинейными элементами, необходимо иметь математические выражения для характеристик элементов. Сами эти характеристики обычно являются экспериментальными, т.е. полученными в результате измерений соответствующих элементов, а затем на этой основе формируются справочные (типовые) данные. Процедуру математического описания некоторой заданной функции в математике называют аппроксимацией этой функции. Существует целый ряд типов аппроксимации: по выбранным точкам, по Тейлору, по Чебышеву и др. В конечном итоге необходимо получить математическое выражение, которое с какими-то заданными требованиями удовлетворяло исходной, аппроксимирующей функции.

Рассмотрим простейший способ: метод выбранных точек или узлов интерполяции степенным полиномом.

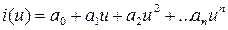
Необходимо определить коэффициенты полинома. Для этого выбирается (n+1) точек на заданной функции и составляется система уравнений:

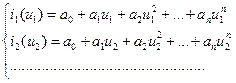
Из этой системы находятся коэффициенты а₀, а₁, а₂, …, а_n.

В выбранных точках аппроксимирующая функция будет совпадать с исходной, в других точках – отличаться (сильно или нет – зависит от степенного полинома).

Можно использовать экспоненциальный полином:

Второй метод: метод аппроксимации по Тейлору. В этом случае выбирается одна точка, где будет совпадение исходной функции с аппроксимирующей, но дополнительно ставится условие, чтобы в этой точке совпадали еще и производные.

Аппроксимация по Батерворту: выбирается простейший полином: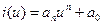

В этом случае можно определить максимальное отклонение ε на краях диапазона.

Аппроксимация по Чебышеву: является степенной, там устанавливается совпадение в нескольких точках и минимизируется максимальное отклонение аппроксимирующей функции от исходной. В теории аппроксимации функций доказывается, что наибольшее по абсолютной величине отклонение полинома f(x)степени п от непрерывной функции ξ(х) будет минимально возможным, если в интервале приближения а ≤ х ≤ b разность

f(x) - ξ(х) не меньше, чем п + 2 раза принимает свои последовательно чередующиеся предельные наибольшие f(x) - ξ(х) = L > 0 и наименьшие f(x) - ξ(х) = -L значения (критерий Чебышева).

Во многих прикладных задачах находит применение полиномиальная аппроксимация по среднеквадратическому критерию близости, когда параметры аппроксимирующей функции f(x) выбираются из условия обращения в минимум в интервале аппроксимации а ≤ х ≤ b квадрата отклонения функции f(x) от заданной непрерывной функции ξ(х), т. е., из условия:

Λ= 1/b-a∫_a[f(x)- ξ(x)]² dx = min . (7)

В соответствии с правилами отыскания экстремумов решение задачи сводится к решению системы линейных уравнении, которая образуется в результате приравнивания к нулю первых частных производных функции Λ по каждому из искомых коэффициентов a_k аппроксимирующего полинома f(x), т. е. уравнений

дΛ ∕дa₀=0; дΛ ∕дa₁=0; дΛ ∕дa₂=0, . . . , дΛ ∕дa_n =0. (8)

Доказано, что и эта система уравнений имеет единственное решение. В простейших случаях оно находится аналитически, а в общем случае — численно.

Чебышев установил, что должно для максимальных отклонений выполняться равенство:

В инженерной практике используется еще так называемая кусочно-линейная аппроксимация – это описание заданной кривой отрезками прямых линий.

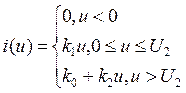
В пределах каждого из линиаризированных участков вольт - амперной характеристики применимы все методы анализа колебаний в линейных электрических цепях. Ясно, что, чем на большее число линеаризированных участков разбивается заданная вольт-амперная характеристика, тем точнее она может быть аппроксимирована и тем больше объем вычислений в ходе анализа колебаний в цепи.

Во многих прикладных задачах анализа колебаний в нелинейных резистивных цепях аппроксимируемая вольт - амперная характеристика в интервале аппроксимации с достаточной точностью представляется двумя или тремя отрезками прямых.

Подобная аппроксимация вольт - амперных характеристик дает в большинстве случаев вполне удовлетворительные по точности результаты анализа колебаний в нелинейной резистивной цепи при «небольших» по величине воздействиях на нелинейный элемент, т. е. когда мгновенные значения токов в нелинейном элементе изменяются в предельно допустимых границах от I = 0 до I = I_мах

<42 43 44 45 464748 >

Дата добавления: 2016-03-15; просмотров: 2568;