Алгоритм отыскания локальных экстремумов функции
| 1. Найти производную заданной функции. 2. Приравнять производную к нулю и, решив полученное уравнение, найти стационарные точки. 3. Исследовав знаки производной слева и справа от каждой стационарной точки (достаточный признак экстремума), сделать заключение о наличии, характере или отсутствии экстремума в этой точке. |
ПРИМЕРЫ:
1. Найдите экстремум функции y = x2. Следуя приведенному алгоритму, запишем: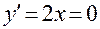 
. Решением полученного уравнения будет единственная стационарная точка х0 = 0. Очевидно, слева от этой точки производная функции будет отрицательна, а справа – положительна. Следовательно, стационарная точка х0 = 0 есть точка минимума данной функции.
2. Найдите экстремум функции y = x3. Аналогично предыдущему примеру запишем: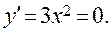 
Очевидно, что слева и справа от единственной стационарной точки х0 = 0 производная функции положительна. Следовательно, в этой точке экстремума нет. В этом можно убедиться и применив достаточный признак № 2. Имеем: 
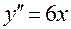и 
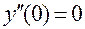, т.е. и этот признак указывает на отсутствие экстремума в этой точке.
Дата добавления: 2016-04-11; просмотров: 1757;