Примеры решения задач. Задача 1.Найдите уравнение касательной к графику функции в точке М (2, 4).
Задача 1.Найдите уравнение касательной к графику функции 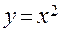 в точке М (2, 4).
в точке М (2, 4).
Решение. Любая прямая, проходящая через точку М, будет иметь уравнение: 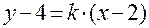 . Очевидно, что и касательная к графику рассматриваемой функции будет иметь такое же уравнение. Неизвестный нам угловой коэффициент k может быть найден, исходя из условия, что угловой коэффициент касательной численно равен значению производной функции, вычисленной в точке касания:
. Очевидно, что и касательная к графику рассматриваемой функции будет иметь такое же уравнение. Неизвестный нам угловой коэффициент k может быть найден, исходя из условия, что угловой коэффициент касательной численно равен значению производной функции, вычисленной в точке касания: 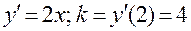 . Таким образом, искомое уравнение можно записать в виде: 4x – y – 4 = 0.
. Таким образом, искомое уравнение можно записать в виде: 4x – y – 4 = 0.
Задача 2.Для функции спроса D (p) = 40 – 2p найдите эластичность спроса по цене при p = 4.
Решение.Используя формулу для эластичности функции, имеем:
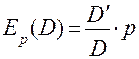 .
.
Подставляя в эту формулу значения: 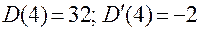 , получим:
, получим:
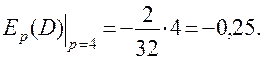
Полученный результат означает, что при возрастании цены на 1%, спрос упадет на 0,25%, т.е. в рассматриваемом случае спрос будет неэластичным.
Основные теоремы о свойствах дифференцируемых функций
| Если функция y = f (x) дифференцируема в точке х = х0, то она непрерывна в этой точке. |
Теорема Ферма
Пусть функция f (x) определена на интервале (a, b) и в некоторой точке х0 этого интервала имеет наибольшее или наименьшее значение. Тогда, если в этой точке существует производная, то она равна нулю, т.е. 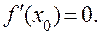
|
Геометрический смысл теоремы Ферма состоит в том, что в точках максимума и минимума функции касательная к ее графику горизонтальна, т.е. составляет нулевой угол с осью абсцисс.
Теорема Ролля
Если функция f (x) непрерывна на отрезке [a, b], дифференцируема на интервале (a, b) и f (a) = f (b), то существует хотя бы одна точка 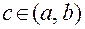 такая, что такая, что 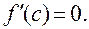
|
Теорема Лагранжа
Если функция f (x) непрерывна на отрезке [a, b], дифференцируема на интервале (a, b), то найдется такая точка 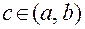 , в которой выполняется условие: , в которой выполняется условие: 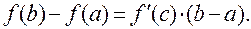
|
Геометрический смысл теоремы Лагранжа состоит в том, что если угловой коэффициент секущей М1М2 равен отношению приращения функции на отрезке [a, b] к длине этого отрезка, то на интервале (a, b) обязательно найдется такая точка c, что касательная, проведенная к графику функции в точке М0 (c, f (c)), будет иметь такой же угловой коэффициент, как у секущей (рис. 6).
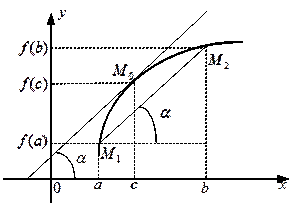
Рис. 6.
Правило Лопиталя
Если функции f (x) и g (x) дифференцируемы в точке х0 и выполняется равенство: 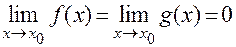 , то справедлива формула:
, то справедлива формула:
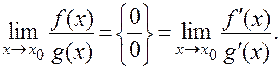
|
Приведенную формулу можно сформулировать в виде правила Лопиталя:
| Предел частного двух дифференцируемых функций в случае неопределенности вида {0/0} равен пределу частного производных этих функций, если этот предел существует. |
Это правило остается верным и в случае, когда 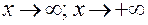 и
и 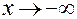 , а также и в том случае, когда под знаком предела имеется неопределенность вида:
, а также и в том случае, когда под знаком предела имеется неопределенность вида: 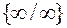 , т.е.:
, т.е.:
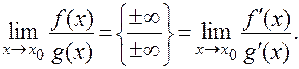
ПРИМЕР: 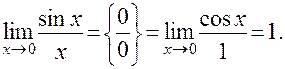
Поскольку неопределенности вида 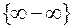 могут быть сведены к неопределенностям вида
могут быть сведены к неопределенностям вида 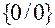 , то к раскрытию таких неопределенностей также можно применять правило Лопиталя. Кроме того, правило Лопиталя после логарифмирования можно применять для раскрытия неопределенностей видов
, то к раскрытию таких неопределенностей также можно применять правило Лопиталя. Кроме того, правило Лопиталя после логарифмирования можно применять для раскрытия неопределенностей видов 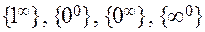 .
.
Дата добавления: 2016-04-11; просмотров: 1927;
