Асимптоты графика функции и их отыскание
Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точки (x, f (x)) графика функции до этой прямой неограниченно уменьшается (стремится к нулю) при неограниченном удалении этой точки от начала координат. Существует три вида асимптот: вертикальная, горизонтальная и наклонная.
Определение. Прямая х = х0 называется вертикальной асимптотой графика функции y = f (x), если точка х0 является точкой разрыва второго рода этой функции.
Таким образом, задача отыскания вертикальных асимптот сводится к задаче отыскания таких точек х0, в которых либо правый, либо левый, либо оба сразу пределы функции бесконечны.
ПРИМЕР: График функции y = 1 / x имеет вертикальную асимптоту х = 0, т.е. ось Oy, т.к.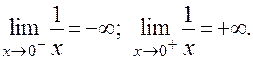 
График этой функции приведен на рис. 10:
Рис. 10.
Определение. Прямая y = A называется горизонтальной асимптотой графика функции y = f (x) при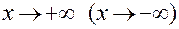 
, если 
.
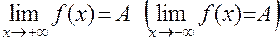Задача отыскания горизонтальных асимптот, очевидно, сводится к нахождению указанных в определении пределов.
ПРИМЕР: График функции y = 1 / x имеет горизонтальную асимптоту y = 0, т.к.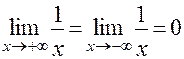 
(рис. 10).
Определение.Прямая y = kx + b называется наклонной асимптотой графика функции y = f (x) при 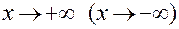, если параметры k и b уравнения этой прямой найдены по формулам:
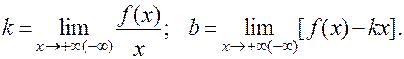
Если хотя бы один из этих пределов не существует, то наклонные асимптоты отсутствуют. Кроме того, наклонные асимптоты имеет смысл искать только в том случае, когда отсутствуют горизонтальные асимптоты.
ПРИМЕР: Для функции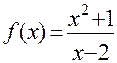 
существует наклонная асимптота с уравнением y = x + 2, т.к. вычисления по формулам определения дают:
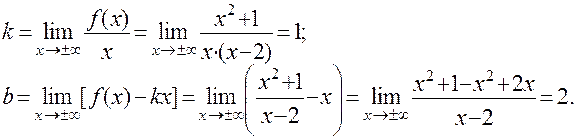
Дата добавления: 2016-04-11; просмотров: 1737;