Основные свойства неопределенного интеграла
Из определения неопределенного интеграла непосредственно вытекают следующие его основные свойства.
1). Производная неопределенного интеграла равна подынтегральной функции, а дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.:
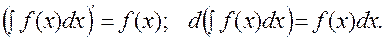
2). Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.:
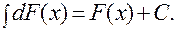
3). Постоянный множитель можно выносить за знак неопределенного интеграла, т.е. если k = const ¹ 0, то:
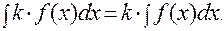
4). Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме неопределенных интегралов от этих функций, т.е.:
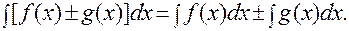
Таблица основных неопределенных интегралов
В приведенной ниже таблице основных неопределенных интегралов часть формул (1÷10) следует из определения интегрирования как операции, обратной дифференцированию, и из таблицы производных простейших элементарных функций. Справедливость остальных формул легко может быть проверена дифференцированием.
1). 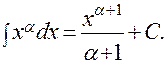 2).
2). 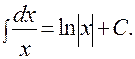
3). 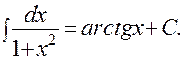 4).
4). 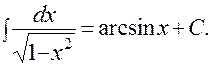
5). 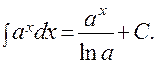 6).
6). 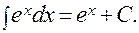
7). 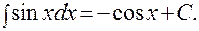 8).
8). 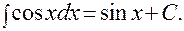
9). 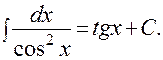 10).
10). 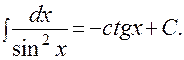
11). 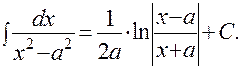
12). 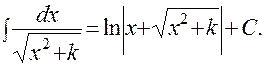
13). 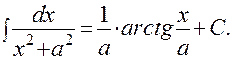
14). 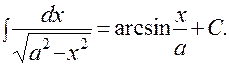
Неопределенные интегралы, содержащиеся в этой таблице, условно называются табличными.
Дата добавления: 2016-04-11; просмотров: 847;
