Метод замены переменной
Во многих случаях удачное введение новой переменной интегрирования позволяет свести операцию нахождения интеграла к непосредственному интегрированию. Такой метод называется методом замены переменной или методом подстановки.
В основе метода замены переменной лежит формула:
|
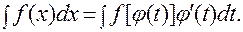
В этой формуле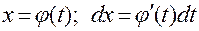 
и есть замена переменной. В результате вычисления интеграла в правой части формулы получится функция, зависящая от аргумента t, поэтому, чтобы вернуться к первоначальной переменной х, нужно в полученном результате провести обратную замену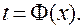 
ПРИМЕРЫ:
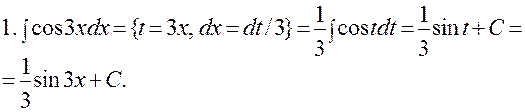
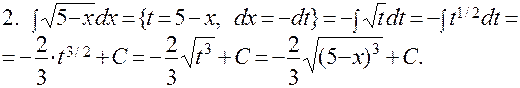
Рациональной тригонометрической функцией от переменных sin x и cos x называется выражение, в котором над этими переменными производятся арифметические действия (сложение, вычитание, умножение и деление).
ПРИМЕР: Выражение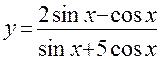 
является рациональной тригонометрической функцией.
Интегрирование рациональных тригонометрических функций сводится к интегрированию рациональных дробей с помощью универсальной тригонометрической подстановки:
|
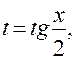
при этом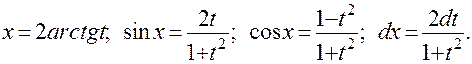 
ПРИМЕР:
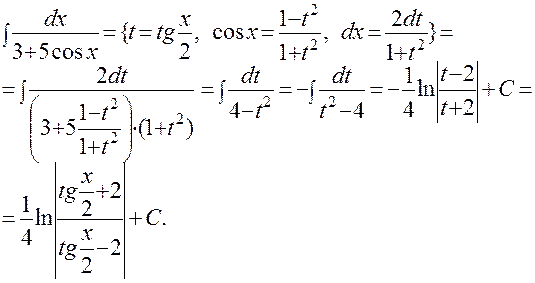
Дата добавления: 2016-04-11; просмотров: 697;