Определенный интеграл

Основные понятия и определения

Пусть функция y = f (x) определена и неотрицательна на отрезке [a, b] и a < b. Разобьем этот отрезок на n произвольных частей точками:

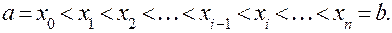
В каждом из полученных отрезков 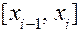выберем произвольную точку 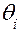, а длину такого отрезка обозначим .

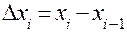Составим сумму σ следующим образом:

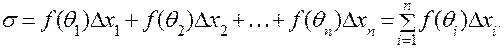
Будем называть такую сумму интегральной суммой для функции f (x) на отрезке [a, b]. Геометрический смысл этой суммы очевиден – это сумма площадей прямоугольников с основаниями 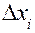и высотами 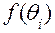. Если через λ обозначить наибольшую из длин 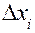и учесть факт, что из условия λ→0 вытекает условие n→∞ , то можно сформулировать следующее определение.

Определение.Если существует конечный предел J интегральных сумм σ при λ→0, то этот предел называется определенным интегралом от функции f (x) по отрезку [a, b] и обозначается следующим образом:

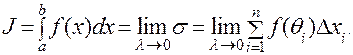
При этом числа а и b называются пределами интегрирования, а функция f (x) – подынтегральной функцией.