Вычисление определенного интеграла способом подстановки
При вычислении определённого интеграла так же приходится применять различные приёмы, в том числе и способ подстановки. Подстановка в определённом интеграле делается аналогично подстановке в неопределённом интеграле, но, кроме того, для получающегося интеграла нужно находить новые пределы интегрирования.
Правило:
1) Определить, к какому табличному интегралу приводится данный интеграл;
2) Определить, какую часть подынтегральной функции необходимо заменить новой переменной, записать эту замену;
3) Вычислить дифференциал новой переменной и выразить через него оставшуюся без замены часть подынтегрального выражения;
4) Найти пределы интегрирования для новой переменной;
5) Выполнить замены под знаком интеграла;
6) Вынести за знак интеграла постоянный множитель;
7) Вычислить полученный табличный интеграл;
8) В полученное его выражение подставить вместо новой переменной сначала верхний предел интегрирования, а затем нижний, из первого результата вычесть второй.
Замечание: В отличие от неопределенного интеграла после подстановки новой переменной и замены пределов интегрировании в определённом интеграле все вычисления проводят с новой переменной и к старой переменной не возвращаются.
Пример: Вычислить:
1. 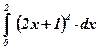 ;
;
Решение:
1) 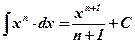 ;
;
2) 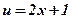 ;
;
3) 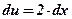 ;
; 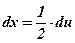 ;
;
4)
| х | 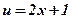
|
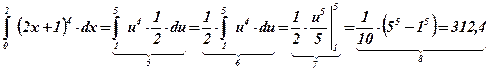
Ответ: 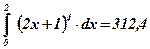 .
.
2. 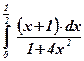 ;
;
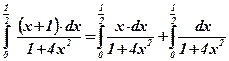 ;
;
1) 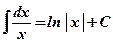 ;
;
2) 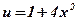 ;
;
3) 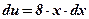 ;
; 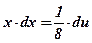 ;
;
4)
| х | 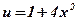
|
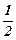
|
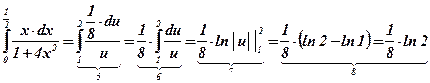 ;
;
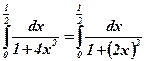 ;
;
1) 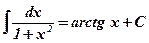 ;
;
2) 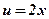 ;
;
3) 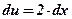 ;
; 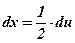 ;
;
4)
| х | 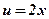
|
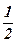
|
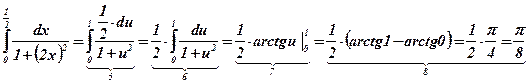 ;
;
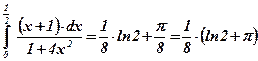 ;
;
Ответ: 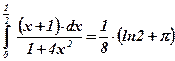 .
.
3. 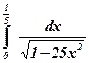 ;
;
1) 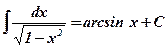 ;
;
2) 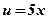 ;
;
3) 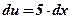 ;
; 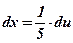 ;
;
| х | 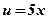
|
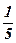
|
4)
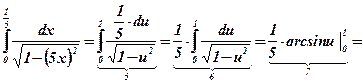
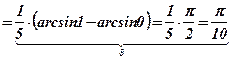
Ответ: 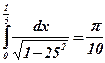 .
.
Упражнения: Вычислить определённые интегралы:
1) 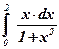 ; ;
| 2) 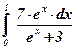 ; ;
| 3) 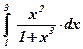 ; ;
|
4) 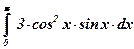 ; ;
| 5) 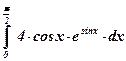 ; ;
| 6) 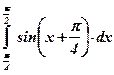 ; ;
|
7) 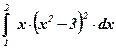 ; ;
| 8) 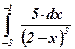 ; ;
| 9) 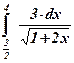 ; ;
|
10) 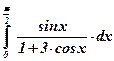 ; ;
| 11) 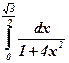 ; ;
| 12) 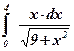 ; ;
|
13) 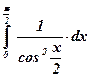 ; ;
| 14) 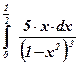 ; ;
| 15) 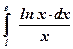 ; ;
|
16) 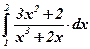 ; ;
| 17) 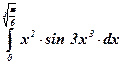 ; ;
| 18) 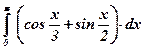 ; ;
|
19) 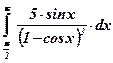 ; ;
| 20) 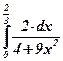 ; ;
| 21) 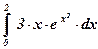 ; ;
|
22) 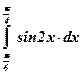 ; ;
| 23) 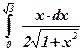 ; ;
| 24) 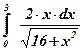 ; ;
|
25) 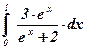 ; ;
| 26) 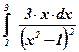 ; ;
| 27) 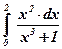 . .
|
Ответы:
1) 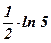 ; ;
| 2) 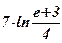 ; ;
| 3) 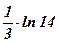 ; ;
| 4) 2; | 5) 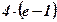 ; ;
| 6) 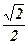 ; ;
|
7) 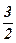 ; ;
| 8) 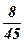 ; ;
| 9) 3; | 10) 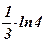 ; ;
| 11) 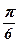 ; ;
| 12) 2; |
| 13) 2; | 14) 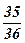 ; ;
| 15) 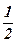 ; ;
| 16) 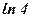 ; ;
| 17) 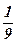 ; ;
| 18) 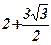 ; ;
|
19) 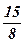 ; ;
| 20) 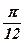 ; ;
| 21) 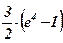 ; ;
| 22) 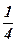 ; ;
| 23) 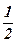 ; ;
| 24) 2; |
25) 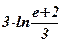 ; ;
| 26) 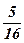 ; ;
| 27) 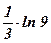 ; ;
|
Дата добавления: 2016-04-11; просмотров: 3981;
