Вычисление площадей плоских фигур с помощью определенного интеграла
Задача №1: Определить площадь фигуры, построенной на отрезке 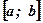 оси абсцисс и ограниченной функцией
оси абсцисс и ограниченной функцией 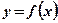 , принимающей отрицательные значения при рассматриваемых значениях аргумента:
, принимающей отрицательные значения при рассматриваемых значениях аргумента: 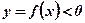 при
при 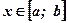 .
.
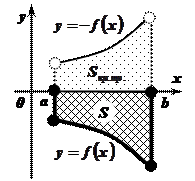 Решение:
Решение:
Площадь данной фигуры равна площади криволинейной трапеции, симметричной данной фигуре относительно оси абсцисс. Криволинейная трапеция ограничена графиком функции, симметричным графику функции 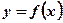 относительно оси Ох, т. е. графиком функции
относительно оси Ох, т. е. графиком функции 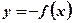 .
.
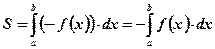
Справка: График функции 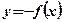 получается симметричным отображением графика функции
получается симметричным отображением графика функции 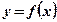 относительно оси Ох.
относительно оси Ох.
Вывод: Площадь фигуры, ограниченной отрицательной функцией 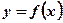 на отрезке
на отрезке 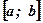 оси абсцисс вычисляется по формуле:
оси абсцисс вычисляется по формуле: 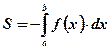
Замечание:Площадь фигуры, построенной на отрезке 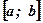 оси абсцисс и ограниченной непрерывной функцией
оси абсцисс и ограниченной непрерывной функцией 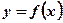 , принимающей неотрицательные (отрицательные) значения при рассматриваемых значениях аргумента, вычисляется по формуле:
, принимающей неотрицательные (отрицательные) значения при рассматриваемых значениях аргумента, вычисляется по формуле: 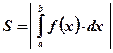 .
.
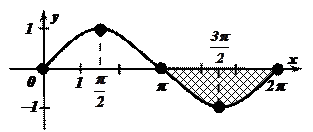 Пример: Вычислить площадь фигуры, построенной на отрезке
Пример: Вычислить площадь фигуры, построенной на отрезке 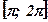 оси абсцисс и ограниченной функцией
оси абсцисс и ограниченной функцией 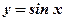 .
.
Решение:
Фигура не является криволинейной трапецией, так как при 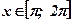
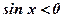 . Воспользуемся формулой
. Воспользуемся формулой
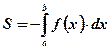 ;
;
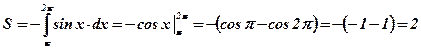 .
.
Ответ: 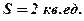
Задача №2: Определить площадь фигуры, построенной на отрезке 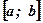 оси абсцисс и ограниченной функцией
оси абсцисс и ограниченной функцией 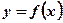 , пересекающей ось абсцисс внутри рассматриваемого отрезка:
, пересекающей ось абсцисс внутри рассматриваемого отрезка:
1) 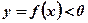 при
при 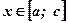 ;
; 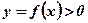 при
при 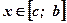 (Рис. 1.);
(Рис. 1.);
2) 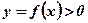 при
при 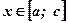 ;
; 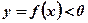 при
при 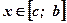 (Рис. 2.).
(Рис. 2.).
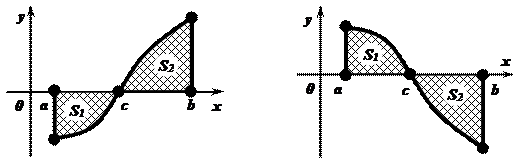 |
Рис. 1. Рис. 2.
Решение:
1) Фигура не является криволинейной трапецией, так как функция, её ограничивающая, принимает и отрицательные и неотрицательные значения при рассматриваемых значениях аргумента.
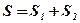 ;
;
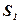 - площадь фигуры, ограниченной функцией
- площадь фигуры, ограниченной функцией 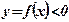 на отрезке
на отрезке 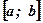 оси абсцисс:
оси абсцисс: 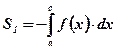 .
.
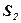 - площадь криволинейной трапеции, ограниченной функцией
- площадь криволинейной трапеции, ограниченной функцией 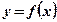 на отрезке
на отрезке 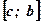 оси абсцисс:
оси абсцисс: 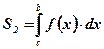 .
.
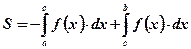
2) Фигура не является криволинейной трапецией, так как функция, её ограничивающая, принимает и отрицательные и неотрицательные значения при рассматриваемых значениях аргумента.
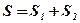 ;
;
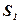 - площадь криволинейной трапеции, ограниченной функцией
- площадь криволинейной трапеции, ограниченной функцией 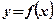 на отрезке
на отрезке 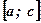 оси абсцисс:
оси абсцисс: 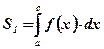 .
.
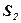 - площадь фигуры, ограниченной функцией
- площадь фигуры, ограниченной функцией 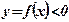 на отрезке
на отрезке 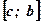 оси абсцисс:
оси абсцисс: 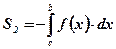 .
.
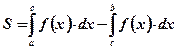
Вывод: Площадь фигуры, построенной на отрезке 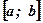 оси абсцисс и ограниченной функцией
оси абсцисс и ограниченной функцией 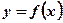 , пересекающей ось абсцисс внутри рассматриваемого отрезка, вычисляется по формуле:
, пересекающей ось абсцисс внутри рассматриваемого отрезка, вычисляется по формуле: 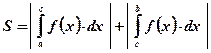 .
.
Пример: Вычислить площадь фигуры, ограниченной функциями: 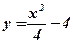 ,
, 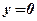 ,
, 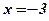 ,
, 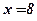 .
.
 Решение:
Решение:
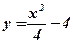 ;
;
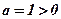 - ветви направлены вверх;
- ветви направлены вверх;
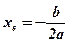 ;
; 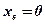 ;
;
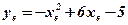 ;
; 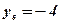 ;
;
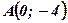 - вершина параболы;
- вершина параболы;
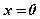 - ось симметрии параболы;
- ось симметрии параболы;
| х | |||||
| у | - 4 | - 3 |
Фигура не является криволинейной трапецией, так как функция 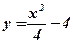 принимает отрицательные значения при
принимает отрицательные значения при 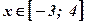 и неотрицательные значения при
и неотрицательные значения при 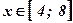 .
. 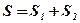 .
.
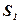 - площадь фигуры, ограниченной функцией
- площадь фигуры, ограниченной функцией 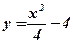 на отрезке
на отрезке 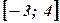 оси абсцисс, вычисляется по формуле
оси абсцисс, вычисляется по формуле 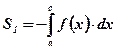 ;
;
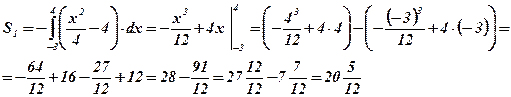
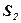 - площадь криволинейной трапеции, ограниченной функцией
- площадь криволинейной трапеции, ограниченной функцией 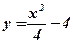 на отрезке
на отрезке 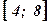 оси абсцисс, вычисляется по формуле
оси абсцисс, вычисляется по формуле 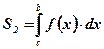 ;
;
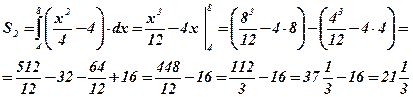
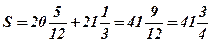
Ответ: 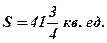
 Задача №3: Определить площадь фигуры, построенной на отрезке
Задача №3: Определить площадь фигуры, построенной на отрезке 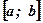 оси абсцисс и ограниченной функциями:
оси абсцисс и ограниченной функциями: 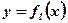 при
при 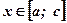 и
и 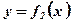 при
при 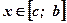 ,
, 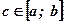 .
.
Решение:
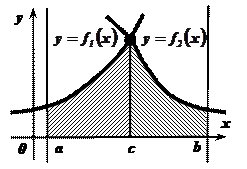
Фигура не является криволинейной трапецией, так как ограничена двумя функциями. Прямой, проходящей через точку пересечения функций 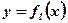 и
и 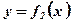 и параллельной оси ординат, фигура разбивается на части
и параллельной оси ординат, фигура разбивается на части 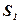 и
и 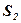 , являющиеся криволинейными трапециями.
, являющиеся криволинейными трапециями.
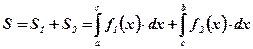 .
.
Задача №4: Определить площадь фигуры, ограниченной функциями 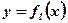 и
и 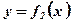 , удовлетворяющими условию
, удовлетворяющими условию 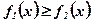 при рассматриваемых значениях аргумента
при рассматриваемых значениях аргумента 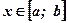 .
.
Решение:
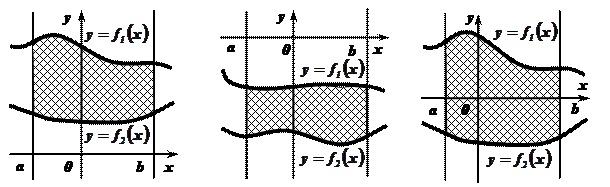 |
Рис. 1. Рис. 2. Рис. 3.
Дата добавления: 2016-04-11; просмотров: 1612;
