Метод подстановки (замены переменной)
Если ни одно из известных преобразований не приводит данный интеграл к такому виду, чтобы можно было применить какую-нибудь формулу интегрирования, приходится прибегать к искусственным приёмам.
Один из широко распространённых приёмов интегрирования – способ подстановки.
Замечание: Способ подстановки применяется в том случае, если под знаком интеграла стоит сложная функция. Промежуточная функция заменяется новой переменой с таким расчётом, чтобы получившийся интеграл был табличным.
Пример: Вычислить неопределённые интегралы:
-
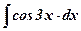 .
.
Решение:
1) К какому табличному интегралу можно привести данный интеграл (на какой табличный интеграл похож данный интеграл)? 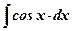 ;
;
2) Какую часть подынтегральной функции надо заменить новой переменной?
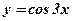 тригонометрическая, линейная функция;
тригонометрическая, линейная функция;  ;
; 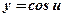 ;
;
3) Вычислим дифференциал новой переменной, чтобы выразить через него оставшийся без замены дифференциал аргумента х: 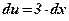 ;
; 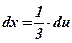 ;
;
4) Выполним замены под знаком интеграла: 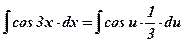 ;
;
5) Вынесем за знак интеграла постоянный множитель: 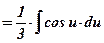 ;
;
6) Вычислим полученный табличный интеграл: 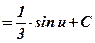 ;
;
7) Выполним обратную замену: 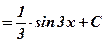 .
.
Ответ: 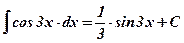 .
.
-
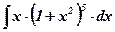 ;
;
Решение:
1) 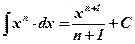 ;
;
2) 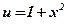 ;
;
3) 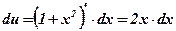 ;
;  ;
;
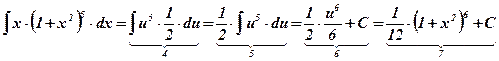 .
.
Ответ: 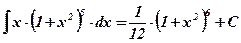 .
.
Правило:
1) Определить, к какому табличному интегралу приводится данный интеграл;
2) Определить, какую часть подынтегральной функции необходимо заменить новой переменной, записать эту замену;
3) Вычислить дифференциал новой переменной и выразить через него оставшуюся без замены часть подынтегрального выражения;
4) Выполнить замены под знаком интеграла;
5) Вынести за знак интеграла постоянный множитель;
6) Вычислить полученный табличный интеграл;
7) Выполнить обратную замену.
Упражнения: Вычислить неопределённые интегралы:
1.  ; ;
| 2. 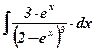 ; ;
| 3. 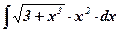 ; ;
|
4. 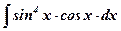 ; ;
| 5. 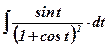 ; ;
| 6. 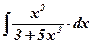 ; ;
|
7.  ; ;
| 8. 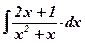 ; ;
| 9. 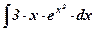 ; ;
|
10. 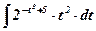 ; ;
| 11. 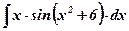 ; ;
| 12. 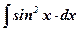 ; ;
|
13.  ; ;
| 14. 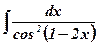 ; ;
| 15. 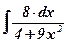 ; ;
|
16. 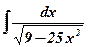 ; ;
| 17. 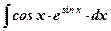 ; ;
| 18. 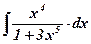 ; ;
|
19. 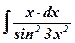 ; ;
| 20. 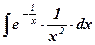 ; ;
| 21. 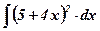 ; ;
|
22. 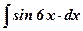 ; ;
| 23. 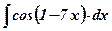 ; ;
| 24. 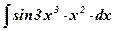 ; ;
|
3. Решение физических задач с помощью неопределённого интеграла
Известно, что скорость 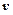 прямолинейного движения точки равна производной от пути
прямолинейного движения точки равна производной от пути 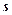 по времени
по времени 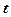 :
: 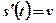 .
.
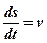 ;
; 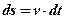 ;
; 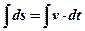 ;
; 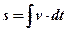 .
.
Вывод: Чтобы найти закон движения точки, надо проинтегрировать скорость прямолинейного движения точки: 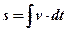 .
.
Пример: Скорость прямолинейного движения точки изменяется по закону 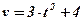 . Найти закон движения
. Найти закон движения 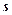 , если за время
, если за время 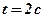 точка прошла 20 м.
точка прошла 20 м.
Решение:
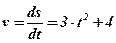 ;
; 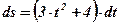 ;
; 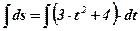 ;
; 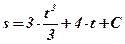 ;
;
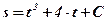 ;
; 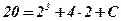 ;
; 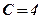 ;
; 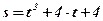 .
.
Ответ: 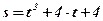 .
.
Упражнения:
- Скорость прямолинейного движения точки изменяется по закону
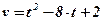 . Найти закон движения точки.
. Найти закон движения точки. - Скорость точки, движущейся прямолинейно, изменяется по закону
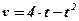 . Найти закон движения точки.
. Найти закон движения точки. - Найти первообразную функции
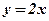 , если известно, что при
, если известно, что при 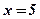 первообразная должна быть равна 14.
первообразная должна быть равна 14. - Скорость прямолинейно движущейся точки задана формулой
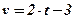 . Найти закон движения точки, если к моменту начала отсчёта она прошла путь 6 м.
. Найти закон движения точки, если к моменту начала отсчёта она прошла путь 6 м. - Скорость прямолинейного движения точки задана формулой
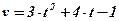 . Найти закон движения точки, если в начальный момент времени она находилась в начале координат.
. Найти закон движения точки, если в начальный момент времени она находилась в начале координат. - Точка движется прямолинейно с ускорением
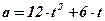 . Найти закон движения точки, если в момент
. Найти закон движения точки, если в момент 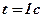 её скорость
её скорость 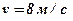 , а путь
, а путь 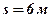 .
. - Точка движется прямолинейно с ускорением
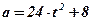 . Найти закон движения точки, если в момент
. Найти закон движения точки, если в момент 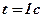 её скорость
её скорость 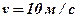 , а путь
, а путь 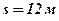 .
. - Точка движется прямолинейно с ускорением
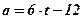 . В момент
. В момент 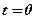 начальная скорость
начальная скорость 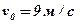 ; расстояние от начала отсчёта
; расстояние от начала отсчёта 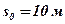 . Найти: скорость и закон движения точки; величину ускорения, скорости и пути в момент
. Найти: скорость и закон движения точки; величину ускорения, скорости и пути в момент 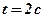 ; момент, когда скорость является наименьшей.
; момент, когда скорость является наименьшей. - Точка движется прямолинейно с ускорением
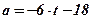 . В момент
. В момент 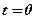 начальная скорость
начальная скорость 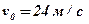 ; расстояние от начала отсчёта
; расстояние от начала отсчёта 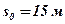 . Найти: скорость и закон движения точки; величину ускорения, скорости и пути в момент
. Найти: скорость и закон движения точки; величину ускорения, скорости и пути в момент 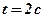 ; момент, когда скорость является наибольшей.
; момент, когда скорость является наибольшей.
Дата добавления: 2016-04-11; просмотров: 731;
