Вычисление интенсивностей лучей, прошедших через пластинку и отражённых от неё. Формулы Эйри.

Спектральное рассмотрение интерференционных явлений. Многолучевая интерференция. Интерферометр Фабри-Перро

Многолучевая интерференция

При отражении света от поверхностей прозрачных пластин вследствие малого коэффициента отражения мы не принимали во внимание лучи, отражённые два или большее число раз. Однако, в случаях, когда интенсивности многократно отражённых лучей близки друг к другу, учёт их вклада в общую интенсивность является обязательным. Реализация упомянутого случая - случая многолучевой интерференции определяется значениями коэффициентов отражения и пропускания.

Вычисление интенсивностей лучей, прошедших через пластинку и отражённых от неё. Формулы Эйри.

Пусть плоская монохроматическая световая волна падает под углом i на поверхность плоскопараллельной прозрачной пластинки (рис 5.6). Показатели преломления пластинки и окружающей среды соответственно будут равны n и n₀.

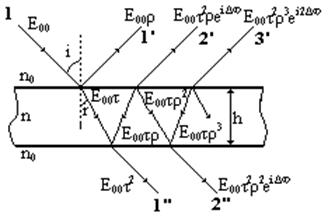
Рис.5.6

Коэффициенты отражения и пропускания по интенсивности обозначим соответственно через R и T. Если поглощением внутри пластинки можно пренебречь, то R+T=1. Ввиду того что потеря полуволны при отражении приводит всего лишь к смещению всей интерференционной картины на полполосы, её в наших расчётах можно не принимать во внимание. Вследствие многократного отражения на границе раздела возникнет совокупность отражённых и прошедших через пластинку параллельных лучей. Представляет интерес рассмотреть многолучевую интерференцию как отражённых, так и прошедших лучей, т.е. найти распределение соответствующих интенсивностей. Для этого надо сложить амплитуды взаимно параллельных лучей с учётом разности хода (фаз) между ними. Очевидно, что разность хода между двумя соседними вышедшими (отражёнными или прошедшими) из пластинки лучами равна

Δd=2hn соs r,

где h - толщина пластинки, r - угол преломления. Этой разнотси хода соответствует разность фаз:

ΔФ=(2π/λ) 2hn соs r,

где λ - длина падающей волны в вакууме.

Обозначим амплитудные коэффициенты отражения (отношение амплитуд отражённой и падающей волн) и пропускания (отношение амплитуд отражённой и падающей волн) через ρ и τ. Пусть амплитуда падающей линейно-поляризованной световой волны будет Е₀₀ (рис.5.6). При каждом прохождении через границу раздела пластинка-воздух амплитуда волны уменьшается в τ раз, а при каждом отражении от такой границы она уменьшается в ρ раз. Вследствие этого амплитуды прошедших через пластинку и отражённых от неё лучей соответственно равны Е₀₀τ², Е₀₀τ²ρ², Е₀₀τ²ρ⁴, Е₀₀τ²ρ⁶ и Е₀₀ρ, Е₀₀τ²ρ, Е₀₀τ²ρ³, Е₀₀τ²ρ⁵,…и т.д. В выражении для амплитуды разность фаз между соседними лучами можно учесть введением соответствующего множителя. Учитывая это, суммарные амплитуды для прошедших и отражённых волн в случае достаточно длинной пластинки будут

∞

Σ_пр=Σ Е₀₀τ²ρ^2Nе^iNΔФ, (5.11)

N=0 ∞

Σ_отр=Е₀₀(ρ+Σ τ²ρ^2N-1е^iNΔФ), (5.12)

N=0

где - N число интерферирующих лучей.

Суммирование, выполненное для случая, когда падение интенсивности складываемых пучков идёт достаточно быстро, приводит к такому результату:

I_прох=[Т²/(1-R)²]* [I_пад/(1+4R/(1- R)²*sin²ΔФ/2)]= Т²*I_пад/((1- R)²+4R*sin²ΔФ/2),(5.13)

I_отр=[[4R*sin²ΔФ/2]/ ((1- R)²+4R*sin²ΔФ/2)]*I_пад ,(5.14)

где Т=τ², R=ρ².

Выражения (5.13) и (5.14) называются формулами Эйри.