III. Методика измерений и расчетные формулы. Общий вид установки представлен на рис.1.

ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СВОБОДНОГО ПАДЕНИЯ

С ПОМОЩЬЮ ФИЗИЧЕСКОГО И МАТЕМАТИЧЕСКОГО

МАЯТНИКОВ

Общий вид установки представлен на рис.1.

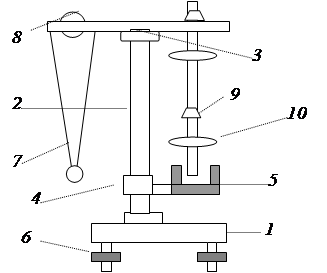
Рис. 1. Лабораторная установка

Установка представлена на рис.1 и включает в себя: основание 1, вертикальную стойку 2, математический и физический (оборотный) маятники, имеющие узлы подвеса на верхнем кронштейне 3, кронштейн 4 для установки фотодатчика, фотодатчик 5.

Основание 1 оснащено регулируемыми ножками 6, которые позволяют произвести выравнивание прибора, и зажимом для фиксации вертикальной стойки.

Вертикальная стойка 2 выполнена из металлической трубы, на которую нанесена миллиметровая шкала.

Математический маятник 7 имеет бифилярный подвес, выполненный из нити, на которой подвешен груз в виде металлического шарика, и устройство 8 для изменения длины подвеса маятника.

Оборотный маятник имеет жесткий металлический стержень с рисками через каждые 10 мм для отсчета длины, две призматические опоры 9, два диска 10 с возможностью перемещения и фиксации по всей длине стержня.

Узлы подвески математического и физического маятников расположены на диаметрально противоположных относительно вертикальной стойки 2 сторонах кронштейна 3.

Кронштейн 4 имеет зажим для крепления на вертикальной стойке 2 и элементы фиксации фотодатчика.

Установка работает от блока электронного секундомера.

III. Методика измерений и расчетные формулы.

Математическим маятником называют систему, состоящую из материальной точки, подвешенной на невесомой нерастяжимой нити, способную совершать колебания в поле силы тяжести.

Физическим маятником называется твердое тело, способное совершать колебания вокруг некоторой оси, не проходящей через его центр инерции.

Возможность определения ускорения свободного падения g по периоду колебаний математического маятника основана на том, что период гармонических колебаний математического маятника зависит только от его длины а и от ускорения свободного падения согласно формуле

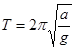. (1)

Следует помнить о том, что данная формула справедлива только в том случае, когда на маятник действует единственная внешняя сила – сила тяжести. Так, если точка подвеса маятника участвует в некотором ускоренном движении, то имеется еще одна внешняя сила – сила инерции.

Измерив длину математического маятника и период малых колебаний Т, можно рассчитать ускорение свободного падения по формуле: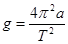

В этих формулах а – расстояние от оси колебания до центра масс колеблющегося тела (шарика).

В условиях данного опыта нельзя пренебречь размерами шарика (d) при определении длины маятника и считать ее равной длине нити l. Разница ( 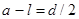) дает относительную погрешность того же порядка, что и приборная погрешность определения Т и на порядок больше приборной погрешности измерения а.

В то же время на установке можно подобрать такую длину нити l, которая позволяет пользоваться приближенной формулой при расчете момента инерции, т. е. считать 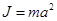, как для материальной точки.

Что бы исключить ошибки при определении а, связанные с неоднородностью шарика, искажаем его формы и невозможностью достаточно точно определить положение оси колебаний, следует проделать два опыта с разной длино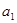й и 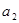, рассчитать g по разност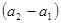и и .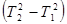

Из формулы (1) получаем:

; .

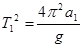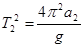Таким образом, ускорение свободного падения равно:

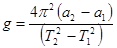. (2)

При малых колебаниях физический маятник совершает гармонические колебания с периодом

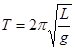, (3)

где L- приведённая длина физического маятника: .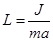

Рис. 2. Оборотный маятник

Введены обозначения m-масса маятника, а- расстояние между точкой подвеса 0 и центром масс С маятника.

Точка 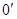, находящаяся на расстоянии приведенной длины L от точки подвеса, называется центром качания физического маятника. Оказывается что всегда .

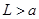Точка подвеса 0 и центр качения 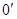обладают свойством взаимозаменяемости: если ось подвеса сделать проходящей через центр качения, то прежняя точка подвеса станет центром, а период колебаний физического маятника не изменится.

В процессе выполнения работы следует определить экспериментально положение центра качения, а также приведённую длину физического маятника.