III. Методика измерений и расчетные формулы. В комплект установки входят: наклонная плоскость с регулируемой высотой, миллисекундомер, набор тел (брусок
ИЗУЧЕНИЕ ДВИЖЕНИЯ ТЕЛ ПО НАКЛОННОЙ ПЛОСКОСТИ
В комплект установки входят: наклонная плоскость с регулируемой высотой, миллисекундомер, набор тел (брусок, шарик, сплошной и полый цилиндры).
Общий вид установки представлен на рисунке. Наклонная плоскость представляет собой доску 1, угол наклона которой можно варьировать, изменяя высоту плоскости с помощью кронштейна 2. На вершине плоскости укреплен электромагнит 3, удерживающий тело. Измерение времени скольжения или скатывания проводится с помощью миллисекундомера 4. Включение секундомера с помощью переключателя 6 размыкает цепь электромагнита, и тело начинает двигаться вниз по наклонной плоскости. При ударе скатывающегося тела о специальную пластинку 5, расположенную вертикально у основания наклонной плоскости, происходит выключение секундомера. Сняв отсчет времени по шкале секундомера, необходимо привести переключатель контакта 6 в исходное положение. Клавиши секундомера 7, отмеченные красной наклейкой, должны быть нажаты, остальные - отжаты.

III. Методика измерений и расчетные формулы
1. Рассмотрим тело (брусок) массой m, находящееся на наклонной плоскости (см. рисунок). Угол наклона плоскости a можно найти из следующих соотношений:

| 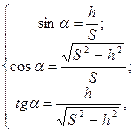 (1) (1)
|
где S - длина наклонной плоскости; h - ее высота, которая является переменной величиной.
Тело будет находиться в покое, если геометрическая сумма действующих на него сил равна нулю:
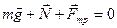
В проекциях на оси координат:
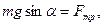
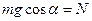
Если учесть, что максимальное значение силы трения покоя равно 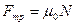 то коэффициент трения покоя
то коэффициент трения покоя 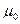 можно найти из соотношения
можно найти из соотношения
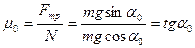 (2)
(2)
где 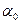 - максимальный угол, при котором тело еще остается в покое.
- максимальный угол, при котором тело еще остается в покое.
Если 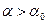 , то
, то 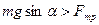 , и тело будет двигаться ускоренно. Согласно второму закону Ньютона
, и тело будет двигаться ускоренно. Согласно второму закону Ньютона
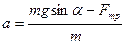
Если учесть, что 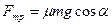 , где
, где 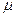 - коэффициент трения скольжения, то
- коэффициент трения скольжения, то
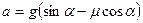 .
.
Отсюда следует, что
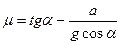
Величину ускорения можно определить, если известны длина пути S1 и время движения t:
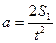
Путь S1 пройденный бруском, находится из соотношения
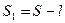 ,
,
где l - длина бруска (размер бруска вдоль наклонной плоскости). Поэтому окончательно коэффициент трения скольжения находим из следующего расчетного соотношения:
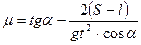 (3)
(3)
Для определения времени движения бруска по наклонной плоскости расчетным путем можно воспользоваться законом изменения полной механической энергии:
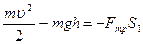
где 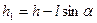 - высота, на которую опускается центр тяжести бруска. Поэтому учитывая, что конечная скорость бруска при равноускоренном движении равна
- высота, на которую опускается центр тяжести бруска. Поэтому учитывая, что конечная скорость бруска при равноускоренном движении равна
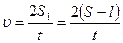 , (4)
, (4)
окончательно получаем:
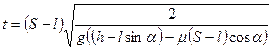 (5)
(5)
2. При рассмотрении движения скатывающихся тел (цилиндр, шар) можно считать, что коэффициент трения качения достаточно мал и поэтому 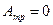 . Поэтому можно воспользоваться законом сохранения механической энергии:
. Поэтому можно воспользоваться законом сохранения механической энергии:
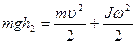 (6)
(6)
где 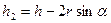 - высота, на которую опускается центр тяжести скатывающегося тела; r и J - радиус и момент инерции скатывающегося тела. Поэтому, с учетом (6) и выражения для конечной скорости скатывающегося тела
- высота, на которую опускается центр тяжести скатывающегося тела; r и J - радиус и момент инерции скатывающегося тела. Поэтому, с учетом (6) и выражения для конечной скорости скатывающегося тела
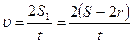 (7)
(7)
получаем, что время скатывания тел равно:
а) для сплошного цилиндра 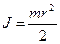 , следовательно
, следовательно
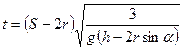 (8)
(8)
б) для шарика ( 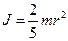 )
)
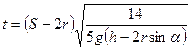 (9)
(9)
в) для отрезка трубы ( 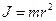 )
)
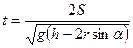 (10)
(10)
Дата добавления: 2016-03-15; просмотров: 2635;
