III. Методика измерений и расчетные формулы. Маятник Обербека (см. рис.) представляет собой крестовину, состоящую из двух одинаковых стержней 1 с делениями

ИЗУЧЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

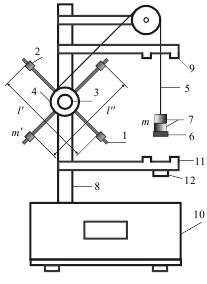Маятник Обербека (см. рис.) представляет собой крестовину, состоящую из двух одинаковых стержней 1 с делениями, прикрепленных крестообразно под углом 90° ко втулке с осью. Расстояние между делениями одинаковое и составляет 1 см. На стержни надеваются одинаковые грузы 2 массой, которые могут закрепляться на разных расстояниях R от оси вращения.

На ось надеты два легких шкива с различными радиусами r₁ и r₂, 3, 4. На шкив наматывается шнур 5, к свободному концу шнура прикреплена чашка 6, на которую можно помещать груз 7 массой m. Под действием груза шнур разматывается, приводя маятник в равноускоренное движение. Положение груза регистрируется по миллиметровой шкале, нанесенной на вертикальную колонну 8. Система измерения времени падения груза включает миллисекундомер и два фотоэлектрических датчика. Верхний датчик 9 вырабатывает электроимпульс начала измерения времени и включает миллисекундомер 10. Нижний датчик 11 вырабатывает сигнал конца работы миллисекундомера и включает тормозной электромагнит 12.

Вращательное движение маятника осуществляется под действием момента силы натяжения шнура. При симметричном расположении грузиков 2 на крестовине указанный момент вращения будет единственным, действующим на прибор, так как момент силы тяжести всего прибора в этом случае равен нулю.

III. Методика измерений и расчетные формулы

Из основного закона динамики вращательного движения следует, что угловое ускорение ε прямо пропорционально моменту M действующих на тело сил (относительно оси вращения) и обратно пропорционально моменту инерции J вращающегося тела относительно той же оси:

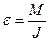. (1)

Чтобы убедиться на опыте в справедливости соотношения (1), нужно проверить выполнение следующих равенств:

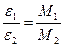при J=const;

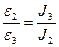при M=const.

Следовательно, необходимо найти отношение угловых ускорений в двух опытах, в которых либо меняется вращающий момент (а момент инерции остается неизменным), либо меняется только момент инерции. Первое может быть достигнуто или изменением массы m, подвешенной к нити системы грузов или переносом нити с одного шкива на другой. Второе - перемещением грузиков m' по стержням крестовины.

В опытах измеряется время t опускания системы грузов с определенной высоты h (h=const):

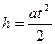, (2)

где a - линейное ускорение грузов.

Поскольку нет проскальзывания нити по шкиву, то угловое ускорение равно ,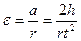

где r - радиус шкива.

В серии опытов, в которых меняется шкив, отношение угловых ускорений равно:

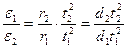, (3)

где d₁ и d₂- диаметры шкивов.

В серии опытов, в которых шкив не меняется (d=const):

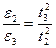. (4)

Вращающий момент M силы натяжения T' с учетом T=T' будет равен:

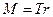. (5)

Силу натяжения нити можно найти из второго закона Ньютона, записав его для движущей массы m:

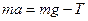. (6)

Решая совместно (5) и (6) с учетом (2), получим:

.

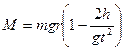Тогда отношение вращающих моментов в двух опытах, когда меняется шкив (при m=const), равно

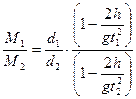. (7)

Момент инерции прибора определяется расчетным путем. Если располагать грузики m' достаточно далеко от оси вращения, чтобы их размеры были малы по сравнению с расстоянием R от оси вращения, то их можно рассматривать как материальные точки. Тогда момент инерции будет определяться по формуле

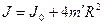, (8)

где R - расстояние центра масс грузика m¢ от оси вращения; J₀ - момент инерции крестовины:

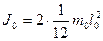. (9)

Введены обозначения: m₀ и l₀ - масса и длина каждого стержня.

Таким образом, отношение моментов инерции системы в серии опытов, где меняется расположение грузов, равно:

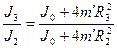(10)