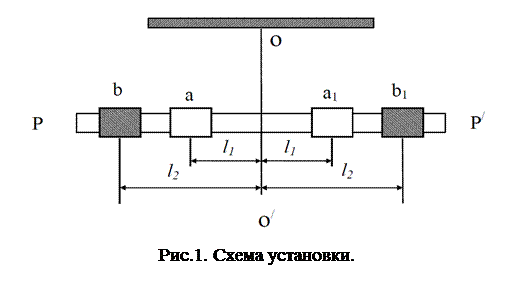
III. Методика измерений и расчетные формулы. Схема установки представлена на рис.1

ОПРЕДЕЛЕНИЕ МОДУЛЯ СДВИГА И МОМЕНТА ИНЕРЦИИ ВРАЩАЮЩЕГОСЯ ТВЕРДОГО ТЕЛА ПРИ ПОМОЩИ КРУТИЛЬНОГО МАЯТНИКА

Схема установки представлена на рис.1. Установка представляет собой кронштейн, укрепленный на основании. Кронштейн снабжен зажимом, в котором фиксируется верхний конец проволоки ОО' из испытуемого материала; для фиксации нижнего конца проволоки служит зажим на основании установки. Для измерения длины проволоки на кронштейне имеется линейка. К нижнему концу проволоки прикреплен горизонтальный стержень PP' со штифтами, на которых закрепляются грузы (цилиндры). Грузы имеют равные массы и могут устанавливаться в двух положениях: aa₁ и bb₁.

III. Методика измерений и расчетные формулы.

При приложении к образцу деформирующей силы, касательной к поверхности, в образце возникает деформация сдвига, при этом закон Гука (справедливый при малых деформациях) для сдвига имеет вид:

,

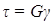где τ — тангенциальное напряжение в образце, γ — угол, на который изменяются прямые углы в образце; данный угол харакетризует относительную деформацию при сдвиге; G — модуль сдвига.

Широко распространенным практическим методом определения модуля сдвига является испытание на кручение. При деформации кручения в образце возникает момент силы упругости:

M = G_кр·φ,

где G_кр — модуль кручения, зависящий от материала и геометрических размеров образца.

Для образца в виде сплошной проволоки длиной L и радиусом R модуль кручения и модуль сдвига связаны соотношением:

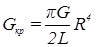, или .

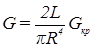Изучаемая система — упругая проволока со стержнем и грузами — представляет собой крутильный маятник. Если стержень повернуть на малый угол и отпустить, то он начнет совершать крутильные колебания с периодом:

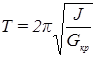. (1)

В данной работе определяются два периода колебаний маятника, соответствующие двум положениям грузов на стержне: в положении aa₁ расстояние от каждого из грузов до оси кручения равно ℓ₁, в положении bb₁ — ℓ₂. Расстояния ℓ₁ и ℓ₂ значительно превышают размеры грузов, поэтому последние можно рассматривать как материальные точки. При размещении грузов в положении aa₁ момент инерции системы равен J₁, а для положения грузов bb₁ — J₂. Значения J₁ и J₂ определяются по формулам:

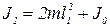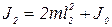, (2)

где J₀ — момент инерции стержня относительно оси OO'.

Из выражений (1) и (2) имеем:

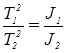, откуда 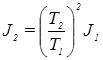. (3)

Из выражений (2) исключаем J₀:

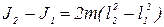(4)

Выражая из (4) J₁ и используя выражение (3), получим:

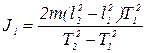. (5)

Модуль кручения G_кр находим из формулы (1) с учетом выражения (5):

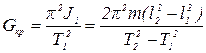(6)

Модуль сдвига:

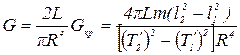(7)