III. Методика измерений и расчетные формулы. Установка ФПТ1-1н представляет собой конструкцию настольного типа,

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ВОЗДУХА

Рис. 1. Схема установки

Установка ФПТ1-1н представляет собой конструкцию настольного типа,

состоящую из двух соединительных корпусов (рис. 1):

1. Приборного блока 1;

2. Блока рабочего элемента 2.

На лицевой панели приборного блока 1 находятся цифровые приборы для измерения давления 3 и расхода 4. В состав блока рабочего элемента 2 входит рабочий элемент, представляющий собой металлический капилляр 5, закрепленный между 9 пневмо-камерами 6. Регулировка расхода воздуха через рабочий элемент осуществляется путем вращения регулятора 7.

III. Методика измерений и расчетные формулы.

Вязкость представляет собой пример так называемых явлений переноса. В упрощенной теории вязкости, которая, тем не менее, охватывает все существенные черты данного явления, используются понятия эффективного диаметра и средней длины свободного пробега молекул газа, которые кратко обсуждаются ниже. Молекулы не все время движутся свободно, а время от времени сталкиваются с другими молекулами. В момент столкновения скорость молекулы испытывает резкое изменение как по величине, так и по направлению. В результате траектория молекулы получается не прямой, а ломаной линией с большим количеством звеньев. Для количественного описания явления Клаузиус ввел понятие средней длины свободного пробега l, т.е. среднего расстояния, которое пролетает молекула между двумя последовательными столкновениями. Для оценки l используется модель твердых шаров [1], с которыми отождествляются молекулы. Диаметр такого шара называется эффективным диаметром молекулы d и совпадает с минимальным расстоянием, на которое сближаются центры двух молекул. Для оценки l предположим, что движется только одна молекула с постоянной скоростью υ – средней тепловой скоростью молекул [2]. Тогда

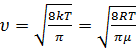. (1)

Вообразим, что с подвижной молекулой жестко связана концентрическая с ней твердая сфера диаметра 2d, которую назовем сферой ограждения молекулы. Между двумя последовательными столкновениями подвижной молекулы ее сфера ограждения описывает цилиндр, длина которого и есть свободный пробег молекулы. Если центр другой молекулы лежит внутри или на боковой поверхности этого цилиндра, то она столкнется с нашей молекулой. В противном случае столкновения не произойдет. Пусть V – объем цилиндра, описываемого сферой ограждения в единицу времени, для которого имеем: V=pd²υ. Среднее число z столкновений движущейся молекулы с остальными молекулами в единицу времени равно среднему числу последних в объеме V, т.е. z=Vn , где n – число молекул в единице объема или концентрация. Следовательно,

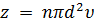. (2)

Путь, пройденный молекулой за единицу времени, равен u. Разделив его на среднее число столкновений z, получим среднюю длину свободного пробега молекулы:

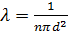. (3)

Строгий расчет с учетом максвелловского распределения молекул по скоростям дает следующий результат [2]

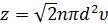, (4)

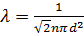. (5)

Наличие внутреннего трения в газах можно проиллюстрировать на следующем примере. Между двумя параллельными пластинками АВ и CD площади S (см. рис. 1) находится воздух или иной газ.

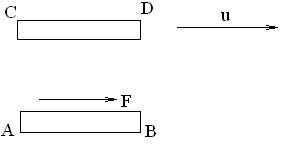
Рис. 2.

При движении пластинки CD появляется сила, действующая на пластинку АВ и направленная в сторону движения. Эта сила и есть сила внутреннего трения. Впрочем, о внутреннем трении можно говорить лишь тогда, когда расстояние между пластинами АВ и CD очень велико по сравнению со средней длиной свободного пробега молекул газа. Тогда от наличия пластин можно отвлечься и говорить о силах, действующих внутри самого газа. Будем представлять себе газ неограниченным и движущимся стационарно плоско-параллельными слоями в горизонтальном направлении. Скорость этого макроскопического движения u меняется в направлении, перпендикулярном к слоям. Это направление примем за ось Х (рис. 2, 3). Таким образом, мы предполагаем, что u=u(x). Рассечем мысленно газ на две половины плоскостью, параллельной слоям и проходящей через некоторую точку x₀. Допустим для определенности, что скорость u(x) возрастает с возрастанием х. Тогда верхняя половина газа будет действовать на нижнюю с силой, направленной вправо, а нижняя на верхнюю – с силой, направленной влево. Это и есть силы внутреннего трения, и их величина определяется формулой Ньютона [2]:

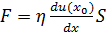(6)

где η - коэффициент вязкости.

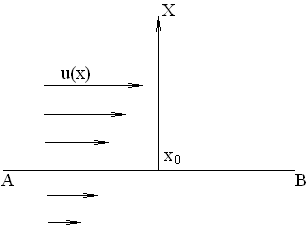
Рис. 3.

С молекулярной точки зрения происхождение сил внутреннего трения объясняется следующим образом. Если бы газ покоился, то все направления скоростей его молекул были бы равновероятны. Средняя скорость и средний импульс каждой молекулы были бы равны нулю. При наличии упорядоченного движения газа средняя скорость молекулы отлична от нуля и равна u=u(x). С этой скоростью связан импульс Р=mu, которым обладает рассматриваемая молекула. Такой импульс условимся называть упорядоченным. Молекулы, лежащие над плоскостью АВ, обладают большим упорядоченным импульсом, чем молекулы, расположенные под ней. Переходя из верхнего полупространства в нижние, молекулы передают часть своего упорядоченного импульса молекулам, с которыми они сталкиваются в нижнем полупространстве. Это проявляется в том, что газ, расположенный ниже плоскости АВ, подвергается действию силы, направленной в сторону скорости u. Аналогично, более медленные молекулы, попадая из нижнего в верхнее полупространство, при столкновениях отнимают часть упорядоченного импульса у молекул, расположенных выше плоскости АВ. В результате газ в верхнем полупространстве испытывает тормозящую силу, направленную против скорости u. Эти силы и являются силами внутреннего трения.

Количественное описание внутреннего трения с помощью рассмотрения потока импульса (который в нашем примере направлен сверху вниз) позволяет получить явное выражение для коэффициента внутреннего трения (или вязкости) [3]:

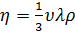. (7)

В (7) использовано соотношение, связывающее плотность газа ρ с массой молекулы m и концентрацией молекул n: ρ=nm.

Для определения коэффициента вязкости воздух продувается через длинный тонкий канал (капилляр) с небольшой скоростью. При малых скоростях потока течение в канале является ламинарным, т.е. поток воздуха движется отдельными слоями, и его скорость в каждой точке направлена вдоль оси канала. Такое течение устанавливается на некотором расстоянии от входа в капилляр, поэтому для достижения достаточной точности эксперимента необходимо выполнение условия r<<l, где r – радиус; l – длина капилляра. В данной установке l=0,1 м, r=0,50 мм. Таким образом, условие малости радиуса капилляра по сравнению с его длиной выполнено. С другой стороны, r достаточно велик по сравнению с l, чтобы был задействован механизм внутреннего трения. Так при условиях, близких к нормальным, для «молекул воздуха» имеем d≈3,7·10^-10 м, и справедлива оценка l~6·10^-8 м.

Для объемного расхода газа Q (т.е. объема газа, протекающего за единицу времени через поперечное сечение канала) справедлива формула Пуазейля [2]:

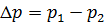. (8)

Это соотношение используется для экспериментального определения коэффициента вязкости газа. Измеряя объемный расход Q и разность давлений (p₁ – p₂) воздуха на концах капилляра длиной l и радиусом r, коэффициент вязкости можно рассчитать по формуле:

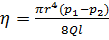. (9)