Термодинамика звука в газе
ИЗУЧЕНИЕ ЗАВИСИМОСТИ СКОРОСТИ ЗВУКА В ВОЗДУХЕ
ОТ ТЕМПЕРАТУРЫ
Термодинамика звука в газе
Звуковая волна в газе представляет собой продольную волну в упругой среде, в которой происходят периодические сжатия и разрежения газа, например воздуха. Как известно из механики, скорость распространения упругих колебаний определяется выражением:
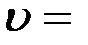
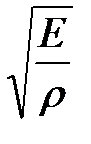 ,
,
гдеЕ – модуль упругости среды, ρ– плотность среды.
| S |
| x |
| dx |
| X |
Рис. 1.
Воспользуемся уравнениями термодинамики для нахождения скорости звука в газе. Выделим мысленно в газе прямоугольный параллелепипед, площадь основания которого S, a высота – x, параллельная вектору скорости распространения волны.
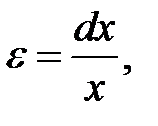
Этот параллелепипед будет испытывать продольную деформацию dx, причём относительная деформация согласно закону Гука:
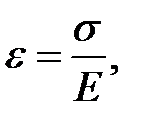
где s – сила давления, испытываемая единицей поверхности выбранного объёма.
В данном случае:
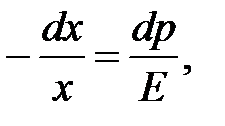
где dp– давление, избыточное над равновесным.
Умножим и разделим левую часть на S:
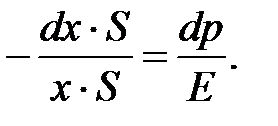
Последнее выражение можно представить в виде:
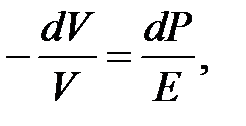
где dV и V –- изменение объема и объём параллелепипеда. Отсюда:
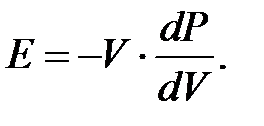
Так как звуковые колебания имеют довольно высокую частоту (сотни и тысячи герц), а теплопроводность газа относительно мала, то смены сжатия и разрежения в газе происходят настолько быстро, что процесс можно считать адиабатным (PVg= const, g – коэффициент Пуассона). Отсюда получаем:
PgVg-1dV + VgdP = 0 ,
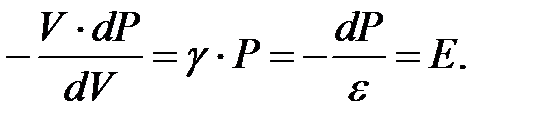
Умножая и деля последнее выражение на молярный объём Vm и ис-пользуя уравнение Менделеева – Клапейрона, получаем окончательное выражение для зависимости скорости звука в газе от температуры:
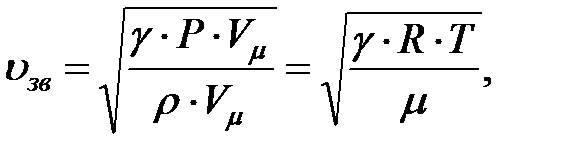 (2)
(2)
где m – молярная масса газа, R – универсальная газовая постоянная, Т – абсолютная температура газа.
Подставляя в последнюю формулу значения величин для воздуха и заменяя абсолютную температуру температурой t по шкале Цельсия, получим удобное для практического применения соотношение:
uзв= 331,6+0,6×t.
Дата добавления: 2016-03-15; просмотров: 2054;
