Приложения определенного интеграла
Вначале рассмотрим три наиболее часто встречающихся случая геометрического приложения определенного интеграла.
Случай 1. Для неотрицательной непрерывной функции y = f (x), заданной на отрезке [a, b], площадь криволинейной трапеции, ограниченной прямыми x = a, x = b, осью Ох и графиком функции y = f (x) (заштрихована на рис. 15), определяется формулой:
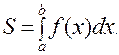
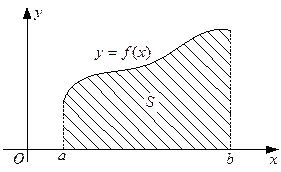
Рис. 15.
ПРИМЕР: Найти площадь криволинейной трапеции, ограниченной графиком функции y = x2, заданной на отрезке [0, 1].
Искомая площадь S будет равна:
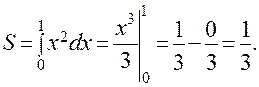
Случай 2. Если на отрезке [a, b] заданы две непрерывные и неотрицательные функции f (x) и g (x), причем всюду на отрезке выполняется неравенство f (x) ≤ g (x), то площадь криволинейной трапеции, ограниченной прямыми x = a, x = b и графиками этих функций (заштрихована на рис. 16), будет определяться формулой:
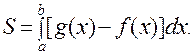
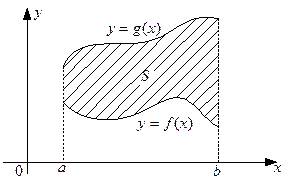
Рис. 16.
ПРИМЕР: Найти площадь фигуры, ограниченной линиями: y1= 1 – x2; y2= x2+ 2, x = 0, x = 1.
Поскольку на заданном отрезке интегрирования [0, 1] выполняется неравенство y2 > y1, искомая площадь будет равна:
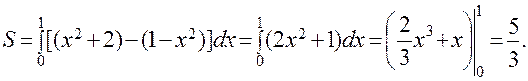
Случай 3.Требуется найти площадь фигуры, ограниченной только графиками функций f (x) и g (x). Для решения этой задачи обычно используется формула случая 2. При этом в качестве пределов интегрирования используются корни уравнения f (x) = g (x), а на первое место в формуле случая 2 ставится та функция, которая не превышает другую на отрезке, определяемом найденными пределами интегрирования. Итак, площадь фигуры, заштрихованной на рис. 17, будет определяться формулой:
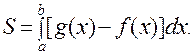
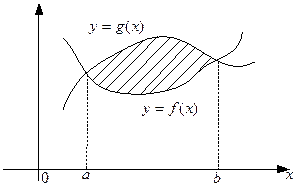
Рис. 17.
ПРИМЕР: Найти площадь фигуры, ограниченной графиками функций: y1 = x2 и y2 = 2 – x2.
Вначале найдем пределы интегрирования, решив уравнение y1 = y2, или x2 = 2 – x2. В результате получим: a = - 1, b = 1. Поскольку на отрезке [-1, 1] выполняется неравенство y2 ≥ y1, искомую площадь найдем по формуле:
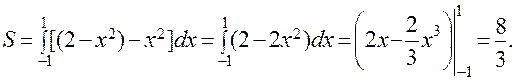
Теперь рассмотрим одно из экономических приложений определенного интеграла. Пусть функция f (t) задает производительность труда в момент времени t, тогда объем продукции, выпущенный за время T, будет определяться формулой:
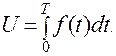
ПРИМЕР: Найти объем продукции, произведенной за 3 часа, если производительность труда определяется функцией 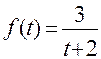 .
.
Этот объем равен:
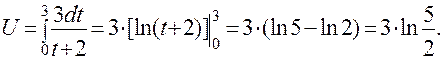
Дата добавления: 2016-04-11; просмотров: 805;
