Достаточное условие дифференцируемости функции двух переменных
| Для того чтобы функция z = f (x, y) непрерывная в точке М0 была дифференцируемой в этой точке, достаточно, чтобы эта функция имела конечные частные производные в этой точке и эти частные производные были бы непрерывны в точке М0. |
ПРИМЕР: Для функции  частные производные существуют во всех точках и соответственно равны:
частные производные существуют во всех точках и соответственно равны:  Поскольку они непрерывны во всех точках, то данная функция будет дифференцируемой во всех этих точках.
Поскольку они непрерывны во всех точках, то данная функция будет дифференцируемой во всех этих точках.
Градиентом функции двух переменныхz = f (x, y) называется вектор с координатами  , т.е.:
, т.е.: 
Вектор градиента в данной точке показывает направление максимальной скорости возрастания функциив этой точке. Вторым важным свойством вектора градиента является следующее: вектор градиента в данной точке перпендикулярен касательной к линии уровня, проведенной через эту точку (рис. 21):

Рис. 21.
ПРИМЕР:Найдите координаты вектора градиента функции  в точке М (2, 2).
в точке М (2, 2).
Найдем значения частных производных заданной функции в заданной точке:

Таким образом, можно записать: 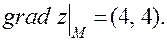
Частные производные и полные дифференциалы
Второго порядка
Пусть имеется функция двух переменных z = f (x, y), которая в каждой точке своей области определения Х имеет частные производные  и
и  . Эти производные (назовем их производными первого порядка), в свою очередь можно рассматривать как некоторые функции двух переменных
. Эти производные (назовем их производными первого порядка), в свою очередь можно рассматривать как некоторые функции двух переменных  и
и 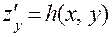 .
.
Частными производными второго порядка функции z = f (x, y) называются частные производные от частных производных первого порядка этой функции. Они могут иметь вид:

Первые две из них принято называть повторными или просто вторыми частными производными функции z = f (x, y), а две других называются смешанными частными производными.
Если функция z = f (x, y) непрерывна на множестве Х и имеет на этом множестве непрерывные смешанные производные, то значения смешанных производных не зависят от порядка их вычисления, т.е. 
|
Дифференциалом второго порядка функции z = f (x, y) называется величина:
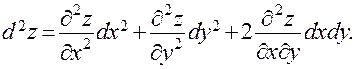
|
Заметим, что по своей структуре дифференциал второго порядка функции двух переменных представляет собой квадратичную форму относительно дифференциалов аргументов, т.е. может быть записан в виде:
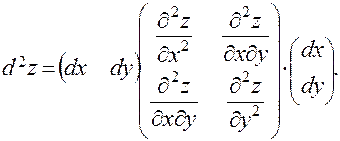
Дата добавления: 2016-04-11; просмотров: 1733;
