Признак сравнения рядов
Если для всех n Î N выполняется неравенство an £ bn, то, если сходится ряд 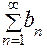 , то сходится и ряд , то сходится и ряд 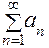 , если
же расходится ряд , если
же расходится ряд 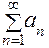 , то расходится и ряд , то расходится и ряд 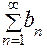 . .
|
ПРИМЕРЫ:
1. Исследовать сходимость ряда  . Поскольку для всех n Î N выполняется неравенство
. Поскольку для всех n Î N выполняется неравенство 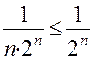 , а геометрический ряд
, а геометрический ряд 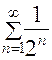 сходится, т.к.
сходится, т.к.  , то сходится и исходный ряд (по признаку сравнения рядов).
, то сходится и исходный ряд (по признаку сравнения рядов).
2. Исследовать сходимость ряда 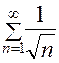 . Поскольку для всех n Î N выполняется неравенство
. Поскольку для всех n Î N выполняется неравенство  , а гармонический ряд
, а гармонический ряд 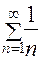 расходится, то по признаку сравнения рядов будет расходиться и исходный ряд.
расходится, то по признаку сравнения рядов будет расходиться и исходный ряд.
Признак Даламбера
Пусть для ряда с положительными членами  существует предел отношения
существует предел отношения 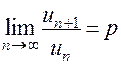 . Тогда:
1). Если p < 1, то ряд сходится.
2). Если p > 1, то ряд расходится.
3). Если p = 1, вопрос о сходимости ряда требует
дополнительных исследований. . Тогда:
1). Если p < 1, то ряд сходится.
2). Если p > 1, то ряд расходится.
3). Если p = 1, вопрос о сходимости ряда требует
дополнительных исследований.
|
ПРИМЕРЫ:
1. Исследуйте сходимость ряда  . Найдем предел:
. Найдем предел:
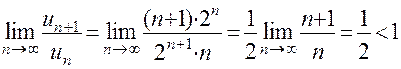 ,
,
Следовательно, на основании признака Даламбера ряд сходится.
2. Исследуйте сходимость ряда  . Найдем предел:
. Найдем предел:
 .
.
Следовательно, на основании признака Даламбера нельзя сделать вывода о сходимости данного ряда, и требуется проведение дополнительных исследований.
Знакочередующимся называется числовой ряд, если его члены поочередно являются положительными и отрицательными, т.е. если он имеет вид: 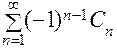 , где для всех n Î N Сn > 0.
, где для всех n Î N Сn > 0.
Для этих числовых рядов существует признак сходимости, который является необходимым и достаточным.
Признак Лейбница
Если для членов знакочередующегося ряда выполняется
неравенство Cn ³ Cn+1 и существует и равен нулю предел
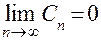 , то ряд этот сходится, а его сумма S £ C1. , то ряд этот сходится, а его сумма S £ C1.
|
ПРИМЕРЫ:
1. Исследуйте сходимость ряда 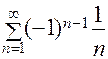 .
.
Для этого ряда выполняется неравенство  , а также равенство
, а также равенство  , поэтому на основании признака Лейбница заключаем, что данный ряд сходится.
, поэтому на основании признака Лейбница заключаем, что данный ряд сходится.
2. Исследуйте сходимость ряда 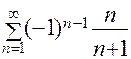 .
.
Убедившись, что для данного ряда выполняется неравенство, противоположное требуемому: 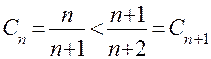 , а также, что
, а также, что
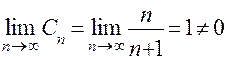 , можно сделать вывод, что данный ряд расходится.
, можно сделать вывод, что данный ряд расходится.
Знакопеременным называется числовой ряд, любой член которого может быть как положительным, так и отрицательным.
Дата добавления: 2016-04-11; просмотров: 866;
