IV. 1. Признаки устойчивости САР

Обратимся теперь к математической стороне вопроса. Любая система автоматического регулирования с входным сигналом (внешней силой) x и выходным сигналом z, имеющая передаточную функцию

,

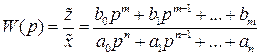может быть описана линейным неоднородным дифференциальным уравнением n-го порядка с постоянными коэффициентами

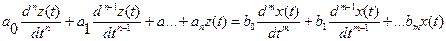(IV.1.1)

Решение этого неоднородного уравнения z(t )состоит из общего решения z_св(t) однородного дифференциального уравнения

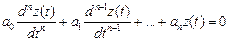(IV.1.2)

и частного вынужденного решения z_вын(t) неоднородного дифференциального уравнения (IV.1.1.)

z(t)= z_св(t)+ z_вын(t).

Из определения устойчивости, данного выше, следует, что устойчивость САР устанавливают в ней, после того как устраняется внешняя сила 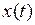, выведшая САР из состояния равновесия. Иными словами, устойчивость системы определяет переходный процесс z_св(t), т.е. решение однородного дифференциального уравнения (IV.1.2.). Таким образом, признаками устойчивости системы являются:

если 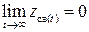, то система устойчива;

если 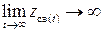, то система неустойчива;

если 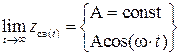, то система нейтральна, т.е. находится на гране устойчивости.

Дифференциальному уравнению (IV.1.2.) соответствует характеристическое уравнение

a_opⁿ+a₁p^n-1+…a_n-1p+a_n=0 , (IV.1.3.)

корни которого могут быть либо вещественными (в том числе нулевыми) либо комплексно-сопряженными (в том числе чисто мнимыми).

Решение дифференциального уравнения (IV.1.2.), как известно, имеет следующий вид

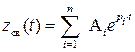_, (IV.1.4.)

где А_i – постоянные интегрирования, определяемые параметрами системы и начальными условиями;

p_i – корни характеристического уравнения (IV.1.3.).

Из этого выражения видно, что переходный процесс z_св(t) состоит из суммы n составляющих, каждая из которых обусловлена соответствующим корнем p_i. При всех вещественных корнях этот корень может быть положительным p_i= 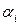( 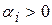), отрицательным 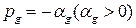или нулевым 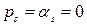. Решение (IV. 1.4) для рассматриваемой составляющей в указанных случаях будет

а) ;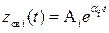

в) ;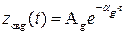

с) .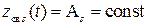

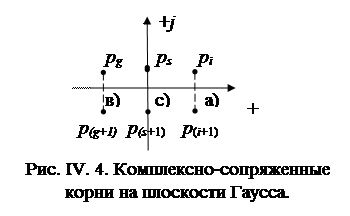
Графики зависимостей а), в), с) представлены на рис. IV.2

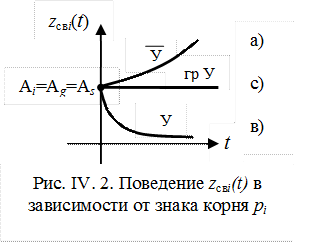
Соответствующие этим зависимостям корни на плоскости корней (плоскости Гаусса) располагаются как показано на рис. IV. 3.

Анализируя рис. IV. 2 и IV.3 и принимая во внимание признаки устойчивости, что устойчивой составляющей z_свg(t)соответствует отрицательный корень p_g, который расположен слева от оси ординат (для кратности обычно говорят – «левый» корень), неустойчивой z_свi(t) – положительный корень p_i (правый корень). Составляющая, определяющая границу устойчивости, характеризуется нулевым корнем, т.е. расположенным на мнимой оси.

При наличии комплексных корней уравнения (IV.1.3) 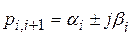в

правую часть формулы (IV.1. 4) будет входить слагаемые

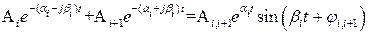(IV. 1.5)

где А 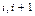и 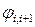– новые постоянные интегрирования.

Если в уравнении (IV.1.3) все корни комплексно-сопряженные, то ясно, что переходный процесс z_св(t) состоит из суммы составляющих вида (IV.1. 5), каждая из которых обусловлена парой комплексно-сопряженных корней p_i,i+1.

Эта пара корней может иметь положительную, отрицательную и нулевую, вещественные части, т.е. быть «правыми», «левыми» и чисто мнимыми корнями (рис. IV. 4)

а) 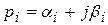, 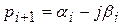или компактнее 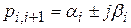, причем ;

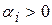в) 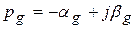, , 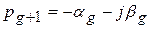, 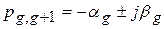причем ;

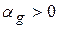с) .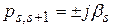

а)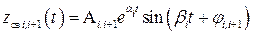

в)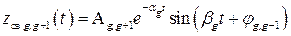

с)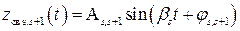

На рис. IV.5 представлены эти решения

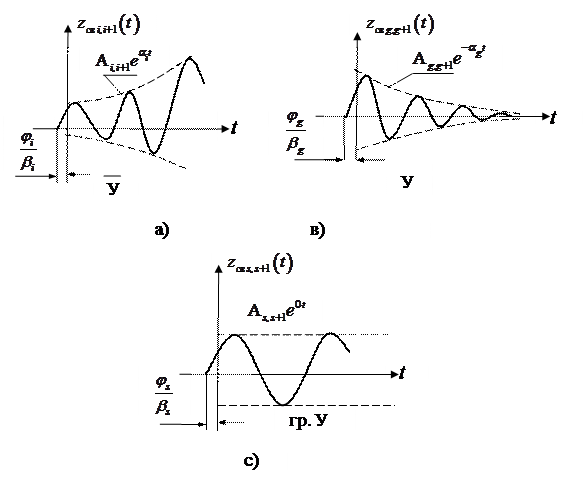
Рис. IV. 5. Поведение 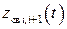в зависимости от

вида вещественной части комплексно- сопряженных корней.

Из всего выше сказанного можно сделать ряд важных выводов.

Если все корни характеристического уравнения (IV.1.3) будут отрицательные вещественные или комплексно-сопряженные с отрицательной вещественной частью (т.е. «левые»), то каждое слагаемое правой части выражения (IV.1. 4.) будет с течением времени уменьшаться и при t→ ∞ , будут стремиться к нулю. Но если каждое слагаемое правой части этого выражения стремиться к нулю при t→ ∞, то и сумма их будет также стремиться к нулю и условие 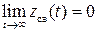будет удовлетворяться, т.е. система будет устойчивой.

Если среди корней характеристического уравнения (IV. 1.3) будет хотя бы один вещественный положительный корень или если это уравнение будет иметь хотя бы одну пару сопряженных комплексных корней с положительной вещественной частью (т.е. будут иметь место «правые» корни), то одно из слагаемых правой части (IV. 1. 4) для вещественного «правого» корня или пары комплексно-сопряженных корней с положительной вещественной частью с течением времени будет неограниченно расти. В этом случае имеет место неустойчивость системы, т.к. .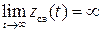

Положим теперь, что корни уравнения (IV.1. 3) «левые» за исключением одного вещественного нулевого (p_s=0) или одной пары чисто мнимых корней 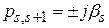. Составляющие переходного процесса, соответствующие «левым» корням при t→ ∞ исчезнут, и останется либо постоянная составляющая 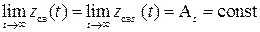в случае нулевого корня либо незатухающая колебательная составляющая 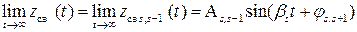, соответствующая паре чисто мнимых корней. В обоих случаях согласно определению признаков устойчивости система находится на границе устойчивости.

Таким образом, необходимым и достаточным условием устойчивости САР является соблюдение того, чтобы все корни характеристического уравнения системы имели отрицательные вещественные части.

Если представить корни характеристического уравнения на комплексной плоскости Гаусса, то для устойчивой системы требуется, чтобы все корни лежали в левой полуплоскости, т.е. были бы «левыми» (рис. IV. 6, а). Остальные состояния устойчивости системы определяются расположением корней, указанных на рис. IV. 6, в, с, d, е.

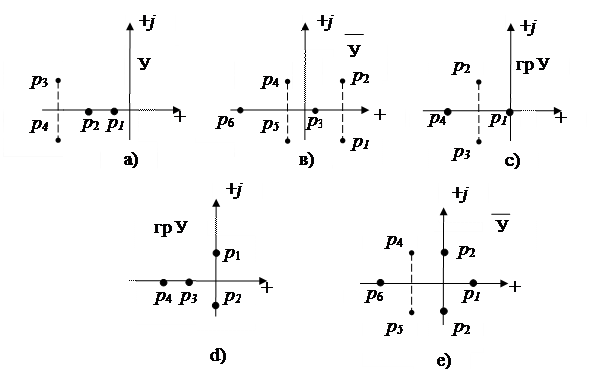
Рис. IV. 6. Расположение корней на плоскости Гаусса для различных состояний устойчивости систем.

Очевидно, что при изменении параметров системы будут изменяться и коэффициенты a_i характеристического уравнения (IV. 1. 3.), а изменение коэффициентов a_i будет вызывать перемещение корней этого уравнения по комплексной плоскости Гаусса. Допустим, определенному набору параметров системы соответствует расположение корней на плоскости Гаусса, показанному на рис. IV. 7.

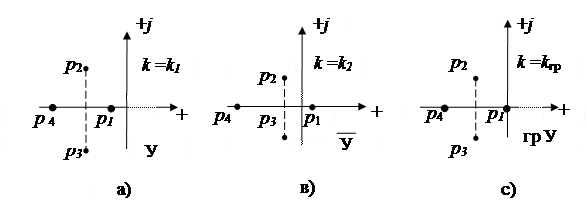
Рис. IV. 7. Расположение корней характеристического уравнения в зависимости от величины параметра k (коэффициента усиления системы).

Положим, что в качестве изменяемого параметра системы взят коэффициент усиления к. При некотором значении k = k₁ расположение корней уравнения (IV. 1. 3.) соответствует случаю устойчивой системы, приведенному на рис. IV. 7,а. Будем теперь увеличивать значение коэффициента k. Расположим корней на плоскости Гаусса при этом будет изменяться. При некотором значении k=k₂>k₁ корень p₁ станет «правым», а система неустойчивой (рис. IV. 7 в). Отсюда следует, что корень p₁, переходя с ростом k из «левого» положения в «правое», при некотором k=k_гр будет находиться на мнимой оси, а система – на границе устойчивости (рис. IV. 7, с). Такое значение параметра (не обязательно коэффициента усиления, а любого, влияние которого на устойчивость мы исследуем), при котором корень (или пара комплексно-сопряженных корней) перемещается на мнимую ось, называется граничным значением параметра (в нашем случае – граничным коэффициентом усиления k_гр).

Итак, мы выяснили, что, определив, все корни характеристического уравнения системы, можно по их (корней) знакам установить устойчивость системы. Однако аналитически находить корни характеристического уравнения уже четвертой степени удается далеко не всегда (лишь для биквадратных уравнений). Поэтому естественным становится желание определить устойчивость системы, не находя корней характеристического уравнения, а используя другие свойства математического описания систем – коэффициенты характеристического уравнения, частотные и другие характеристики систем.

Признаки, позволяющие иметь суждения об устойчивости САР без решения уравнения (IV. 1. 3), получили в теории автоматического регулирования названии критериев устойчивости. К настоящему времени разработано много критериев устойчивости, как алгебраических, так и частотных.