IV. 2. 2. Критерий устойчивости Гурвица

Наиболее распространенная в технической практике форма алгебраического критерия устойчивости известна под названием критерия Гурвица (1895). Этот критерий может быть применен для определения устойчивости как разомкнутых, так и замкнутых САР в зависимости от того, характеристическое уравнение какой из вышеназванных САР принято для исследования.

Ниже рассматриваемый критерий приводится без доказательства.

Для характеристического уравнения (IV. 1. 3) составим квадратную матрицу (таблицу) коэффициентов, содержащую n строк и n столбцов (матрицу Гурвица)

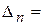
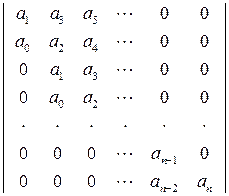(IV. 2. 1)

Эта таблица составляется следующим образом.

По диагонали от левого верхнего до правого нижнего углов выписываются все коэффициенты по порядку от a₁ до a _n._.Каждая строка дополняется коэффициентами с возрастающими слева направо индексами так, чтобы чередовались строки с нечётными и чётными индексами. В случае отсутствия данного коэффициента, а так же если индекс его меньше нуля или больше n, на месте его пишется нуль. Можно заметить, что индексы в столбцах нарастают снизу вверх, поэтому нетрудно понять, что в правом крайнем столбце единственным элементом, отличном от 0, будет нижний элемент a_n .

Главные диагональные миноры или определители матрицы Гурвица

(IV. 2. 1) имеют вид

,

,

,

.

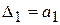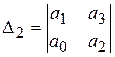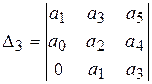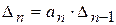Формулировка критерия устойчивости Гурвица обычно дается в следующем виде:

Для устойчивости САР необходимо и достаточно, чтобы при a₀>0 все главные диагональные миноры матрицы Гурвица были бы больше нуля 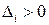(i=1, 2, …n).

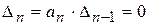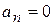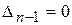Условие нахождения системы на границе устойчивости можно получить, приравняв нулю последний минор при положительности всех остальных главных диагональных миноров. Это условие распадается на два условия: и . Первое условие 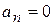свидетельствует о том, что характеристическое уравнение имеет один нулевой корень, это соответствует границе устойчивости апериодического типа, а второе 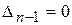говорит о наличии пары чисто мнимых корней и существовании колебательной границы устойчивости.

Если нас интересует граничное значение какого-то параметра (например, коэффициента усиления k_гр), при котором САР становится нейтральной, то его можно найти из выражения

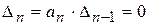. ( IV. 2. 2)

Для часто встречающихся на практике конкретных случаев условия устойчивости Гурвица имеют следующий вид.

Уравнение первого порядка.

Характеристическое уравнение САР в этом случае представляется следующим образом

.

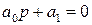Здесь матрица Гурвица совпадает с ее первым диагональным минором .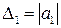

Следовательно, необходимым и достаточным условием устойчивости по Гурвицу является положительность коэффициентов a₀ и a₁.

Уравнение второго порядка.

Характеристическое уравнение здесь таково

,

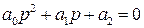поэтому матрица Гурвица имеет вид

.

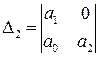Запишем необходимые и достаточные условия устойчивости Гурвица

.

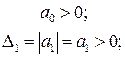
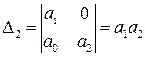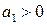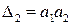Поскольку , то будет положительным только при 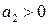и, значит, САР будет устойчива при положительности всех коэффициентов а₀, a₁ и a₂.

Как уже говорилось выше, для САР первого и второго порядков необходимые условия устойчивости Стодолы (т.е. положительность коэффициентов характеристических уравнений) является, как следует из критерия Гурвица, и достаточными.

Уравнение третьего порядка.

Для характеристического уравнения третьего порядка

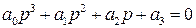
матрица Гурвица имеет вид

.

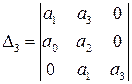Необходимые и достаточные условия устойчивости Гурвица таковы:

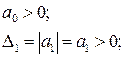
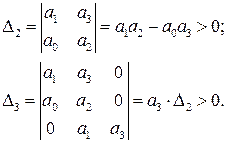
Поскольку по Гурвицу для устойчивости системы все миноры должны быть положительными, из последнего неравенства (если 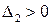) обязательно следует 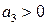. Обратимся теперь ко второму главному диагональному минору 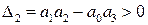. Так как мы установили, что 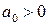, 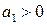и 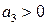, то в этом выражении второе слагаемое всегда положительное, а сам минор 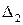может быть положительным только при 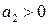. Итак, для устойчивости САР третьего порядка мы получили необходимые условия, выражающиеся в положительности всех коэффициентов характеристического уравнения. Однако, этих условий недостаточно, т. к. из второго минора 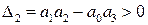видно, что при положительности всех коэффициентов рассматриваемый минор будет положительным только тогда, когда первое слагаемое больше второго. Таким образом, в САР третьего порядка для устойчивости к необходимым условиям добавляется еще условие достаточности

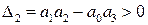. (IV. 2.3)

Уравнение четвертого порядка.

Для САР четвертого порядка уравнение (IV. 1.3) имеет вид

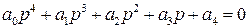
и тогда матрица Гурвица выглядит следующим образом

.

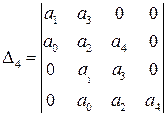Выпишем, как обычно, условия устойчивости по Гурвицу

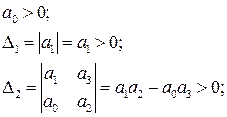
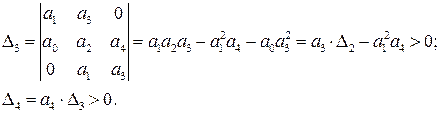
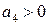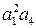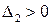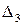При всех положительных минорах последнее неравенство выполняется лишь при и тогда в предпоследнем неравенстве второе слагаемое положительно. При минор будет положительным только при 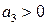. Отсюда следует, что 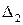будет положительным пр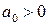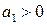и , и 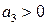, только при .

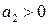Итак, необходимые условия устойчивост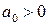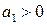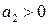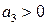и , , , и 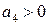мы установили. Сюда необходимо добавить достаточное условие

,

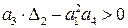которое включает в себя требование

.

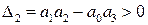Применение критерия Гурвица для исследования устойчивости САР пятого и больших порядков нецелесообразно, т. к. приводит к громоздким вычисления по разрешению миноров, т.е. раскрытию определителей больших порядков. В таких случаях рекомендуется использовать частотные критерии.