IV. 3. 3. 1. Критерий Найквиста для устойчивых разомкнутых САР

Если разомкнутая САР устойчива, то ее характеристическое уравнение А(р) = 0 содержит все n корней в левой полуплоскости. Тогда, согласно принципу аргумента получается

.

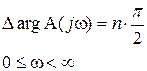Для того, чтобы замкнутая САР была устойчивой, нужно, чтобы ее характеристической уравнение А(р)+В(р) = 0 также содержало все n корней в левой полуплоскости, и, следовательно

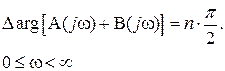
В этом случае согласно (IV. 3. 7) следует, что

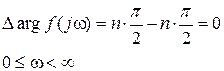, (IV. 3. 8)

т.е. при устойчивой разомкнутой системе изменение аргумента вспомогательного вектора 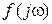с изменением частоты 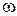от 0 до ∞ равно нулю.

Рассмотрим кривую, которую конец вспомогательного вектора 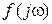описывает при изменении частоты 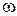от 0 до ∞. Эта кривая, во-первых, подчиняется условиям (IV. 3. 6), а, во-вторых, может проходить либо не охватывая (рис. IV. 13, а), либо охватывая (рис. IV 13, в) начало координат.

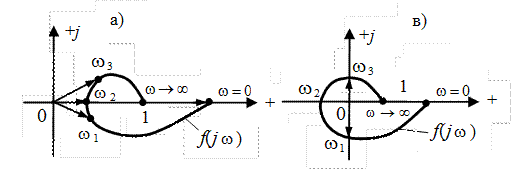
Рис. IV. 13. Положение кривой 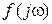относительно

начала координат.

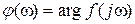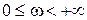Обратим внимание на то, как изменяется аргумент вспомогательного вектора при в обоих случаях. На рис. IV. 13,а, когда кривая не охватывает начало координат, аргумент 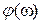, равный нулю при 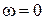, с ростом частоты принимает последовательно значения 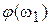(максимальная отрицательная величина) 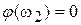, 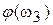(максимальная положительная величина), 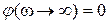. Таким образом, изменение аргумента вектора 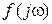в этом случае при 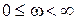равно нулю.

В случае, когда кривая 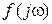охватывает начало координат (рис.IV.13,в), аргумент рассматриваемого вектора

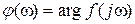
при росте частоты 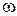от 0 до 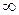изменяется следующим образом: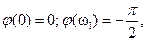

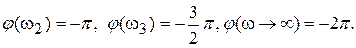
Следовательно, в этом случае

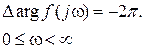
Отсюда, принимая во внимание соотношение (IV. 3.8), можно сказать:

Для устойчивости замкнутой САР при устойчивой разомкнутой системе необходимо и достаточно, чтобы кривая, образованная концом вектора 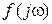, начинаясь на действительной оси, при росте частоты от 0 до 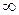не охватывала начало координат.

Поскольку ранее мы условились, что

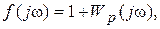(IV.3.9)

т.е. при одинаковых мнимых частях действительная часть АФХ разомкнутой САР W_p 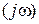сдвинута относительно действительной части 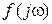на единицу влево и рис. IV. 13 для 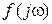можно перестроить для АФХ разомкнутой САР W_p 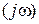следующим образом:

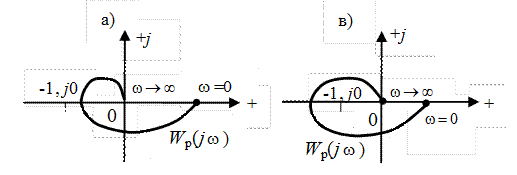
Рис. IV. 14. Положение W_p 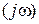относительно

критической точки с координатами (-1, j0).

Если ранее речь шла об охвате или не охвате кривой 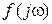начала координат, то, очевидно, теперь (рис. IV. 14.) надо следить за охватом или не охватом кривой W_p 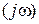критической точки (-1, j0). Поэтому критерий Найквиста окончательно сформулируем в следующем виде:

Для устойчивости замкнутой САР при устойчивой разомкнутой системе необходимо и достаточно, чтобы АФХ разомкнутой САР W_p 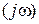, начинаясь на действительной оси, при росте частоты 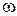от 0 до ∞ не охватывала точки (-1, j0).

Очевидно также, что если W_p 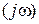, с ростом частоты 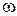от 0 до ∞ охватывает точку (-1, j0), то система в замкнутом состоянии неустойчива. Ну и, наконец, если W_p 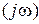проходит через точку (-1, j0), то система находится на границе устойчивости.

АФХ разомкнутой САР W_p 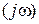, как комплексную функцию можно представить либо в декартовой

,

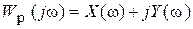либо в показательной форме

.

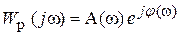Поэтому любой граничный параметр, соответствующий случаю нахождения САР на границе устойчивости, например, граничный коэффициент усиления k_гр, можно определить либо из соотношений

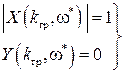
(здесь под 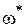понимается то значение частоты, при которой фазовый угол 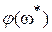становится равным 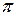), либо следующим образом

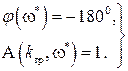
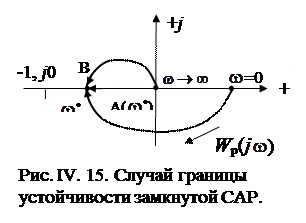
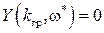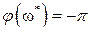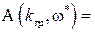
В самом деле, из рис. IV. 15 видно, что в случае границы устойчивости в точке (-1, j0) , , 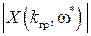=1.