IV. 4. Запасы устойчивости

Устойчивость является необходимым условием нормального функционирования САР. В п. IV. 3. 1 было показано, что (при устойчивой разомкнутой САР) если АФХ разомкнутой системы не охватывает критической точки (-1, j0), то САР в замкнутом состоянии устойчива (кривая 1 на рис. IV. 25), а если указанная АФХ проходит через т. (-1, j0), то замкнутая САР находится на границе устойчивости (кривая 2 на рис. IV. 25).

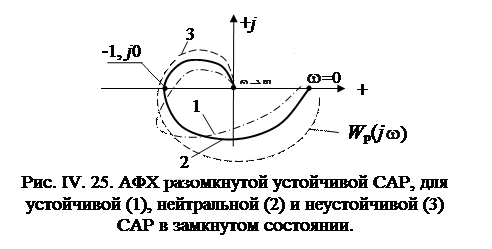
Отметим при этом, что чем ближе находится кривая 1 к критической точке (-1, j0), тем менее устойчивой становится замкнутая САР. Поскольку положение АФХ 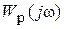на плоскости Гаусса определяется параметрами системы (коэффициентами усиления, постоянными времени и т.п. звеньев), то расположение кривых 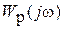вблизи критической точки может привести к ошибочным выводам об устойчивости САР. В самом деле, пусть в исходном состоянии параметры САР таковы, что отвечающая им кривая АФХ заняла положение 1. Однако, со временем в процессе эксплуатации параметры САР изменяются, и соответствующая этим измененным параметрам кривая 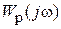уже станет охватывать т. (-1, j0), т.е. займет положение 3. Это означает, что со временем САР, рассчитанная как устойчивая, станет неустойчивой.

Этой ситуации не возникнет, если САР работае6т не вблизи границы устойчивости, а в достаточном удалении от нее. Иначе говоря, САР должна обладать некоторым запасом устойчивости, обеспечивающим работоспособность ее в различных условиях эксплуатации.

Если устойчивость замкнутой системы оценивается критерием Найквиста по расположению АФХ разомкнутой системы относительно критической точки, то в качестве меры оценки запаса устойчивости можно принять расстояние между АФХ 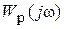и критической точки (-1, j0). Но положение АФХ 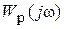на комплексной плоскости для каждого значения частоты 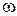характеризуется фазой и модулем. Именно поэтому вводят понятия запасов устойчивости по модулю (амплитуде) и фазе.

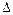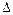Запас устойчивости по модулю (рис. IV. 26, а) характеризует линейное удаление АФХ от критической точки в направлении действительной оси. Величины H₁ и H₂ является мерой оценки запаса устойчивости по модулю двух различных систем с разными АФХ. Иногда вместо этих величин используются величины, с ними связанные, например, вместо 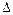H₂ применяется 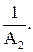Наибольший запас устойчивости по модулю (амплитуде) на рис. IV. 26, а соответствует величине 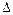H₁ . Из графика видно что системы,

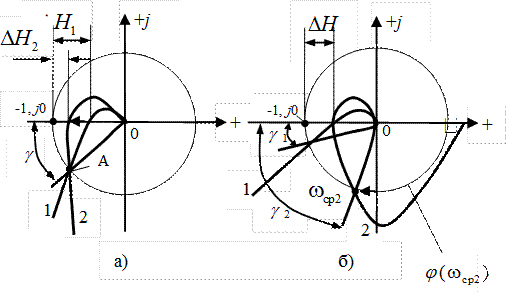
Рис. IV. 26. Запасы устойчивости.

обладающие амплитудно-фазовыми характеристиками 1 и 2 и одинаковым запасом устойчивости по фазе 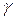(см. ниже), потеряют устойчивость при различных приращениях коэффициента усиления. Для этого, чтобы АФХ 2 прошла через критическую точку и система оказалась на границе устойчивости, ее коэффициент усиления должен получив приращение меньше, чем в случае кривой 1. 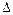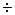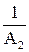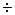Вообще-то для хорошо спроектированной системы запас устойчивости по модулю должен быть H = 0.5 0.9 (в терминах = 2 10).

Запас устойчивости по фазе (рис. IV. 26,б) характеризует угловое отстояние АФХ 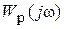по дуге окружности единичного радиуса от критической точки и определяется углом между отрицательным направлением действительной оси и лучом, поведенным из начала координат в точку пересечения АФХ 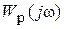с окружностью единичного радиуса,

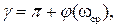
где 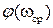- фазовый угол АФХ 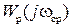, т.е. при 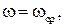когда модуль 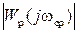равен 1.

В нашем случае, как это видно из рис. IV. 26,б, 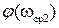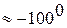, поэтому запас устойчивости по фазе 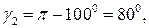т.е. больше нуля. Система с характеристикой 1 имеет меньший запас устойчивости по фазе 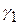по сравнению с системой, обладающий характеристикой 2 и запасом устойчивости по фазе 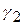. При изменении параметров системы, например, коэффициента усиления, и, следовательно, формы 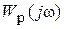, в направлении приближения к критической точке система с меньшим запасом устойчивости по фазе 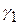потеряет устойчивость при меньшей величине приращения параметра (например, коэффициента усиления) по сравнению с системой, имеющей запас устойчивости по фазе 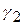. Нетрудно понять, что при переходе системы из устойчивой в неустойчивую, запас устойчивости по фазе из положительного превратится в отрицательный, проходя на границе устойчивости через значение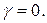

Для хорошо рассчитанных, т.н. «качественных» систем, запас устойчивости по фазе бывает обычно

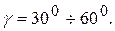
IV.5.Практикум.