IV. 3. 4. Логарифмический критерий устойчивости.

Логарифмический критерий – частотный критерий, позволяющий судить об устойчивости замкнутой САР по виду логарифмических частотных характеристик ЛАЧХ и ЛФЧХ разомкнутой системы. По сути дела здесь речь идет об интерпретации амплитудно-фазового критерия устойчивости Найквиста в логарифмической форме. Соответствующим точкам и значениям АФХ системы, очевидно, будут соответствовать вполне определенные точки и значения ЛАЧХ и ЛФЧХ.

Рассмотрим сначала устойчивую разомкнутую САР. В этом случае при нахождении замкнутой САР на границе устойчивости АФХ разомкнутой системы будет иметь вид, изображенной на рис.IV.15. При этом получается, что

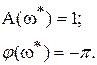
В данном случае границы устойчивости замкнутой САР частота 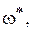при которой 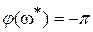, совпадает с частотой среза 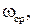при которой 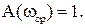Понятно, что в общем случае эти частоты могут не совпадать.

Следовательно, ЛАЧХ на этой частоте будет равна

Таким образом, точке В АФХ разомкнутой системы, изображенной на рис. IV. 15, соответствуют точки В₁ и В₂ на ЛАЧХ и ЛФЧХ, соответственно, показанные на рис. IV. 20.

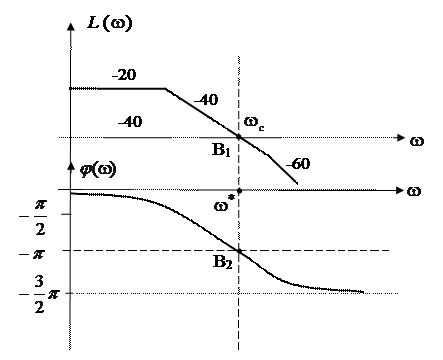
Рис. IV. 20. Логарифмические характеристики разомкнутой САР, соответствующие АФХ рис. IV. 15.

Амплитудно-фазовые характеристики, ЛАЧХ и ЛФЧХ устойчивых разомкнутых систем, соответствующие устойчивым системам в замкнутом состоянии, приведены на рис. IV. 21.

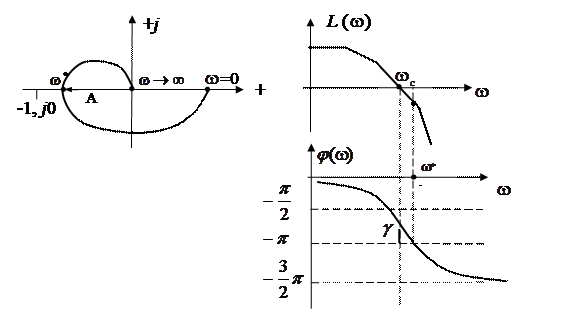
Рис. IV. 22 Устойчивая разомкнутая САР, устойчивая

и в замкнутом состоянии.

При 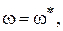когда 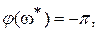видно, что А < 1, поэтому L(A<1)<0. Помимо этого из данного рисунка ясно, что на чистоте среза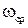 проходит выше линии на угол .

Аналогичные характеристики, соответствующие неустойчивым системам в замкнутом состоянии, приведены на рис. IV. 22.

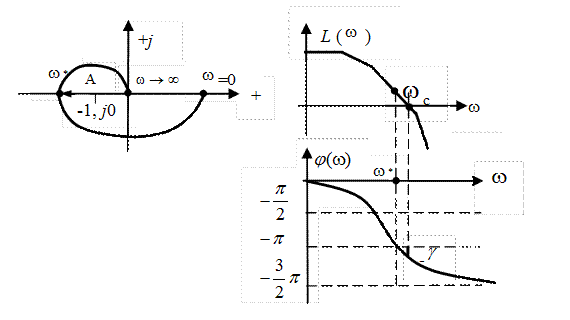
Рис. IV. 22. Устойчивая разомкнутая САР, неустойчивая в замкнутом состоянии.

При 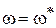, когда 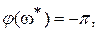видно, что А>1, поэтому L(A>1)>0. кроме того, из рис. IV. 22 очевидно, что на чистоте среза 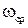ФЧХ 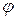( 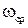) проходит ниже линии - 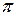на угол .

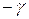Отсюда можно так сформулировать логарифмический критерий устойчивости:

для устойчивой разомкнутой САР система в замкнутом состоянии будет устойчива, если ФЧХ разомкнутой САР на частоте среза 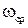проходит выше линии 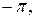и неустойчива, если ниже линии .

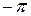В случае же неустойчивой разомкнутой САР надо ориентироваться на формулировку Цыпкина критерия Найквиста (п. IV. 3. 3. 2). В п. IV. 3. 3. 2 принимался во внимание отрезок действительной оси 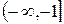, где модуль АФХ разомкнутой системы А >1, что для ЛАЧХ соответствует случаю L(A>1)>0, т.е. положительным значением ЛАЧХ. Кроме того, отметим, что положительному переходу, т.е. сверху вниз, при росте частоты амплитудно-фазовой характеристикой разомкнутой системы отрезка действительной оси в критерии Найквиста 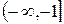, в логарифмическом критерии соответствует переход снизу вверх при росте частоты фазовой частотной характеристикой разомкнутой САР линии 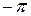на участке, где 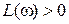. Отсюда, логарифмический критерий устойчивости для неустойчивых разомкнутых САР читается следующим образом:

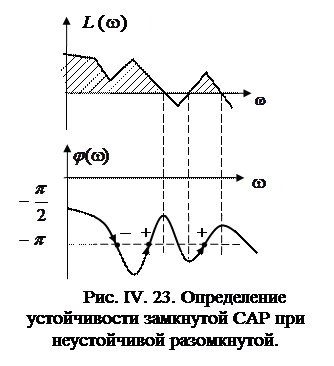
для устойчивости системы в замкнутом состоянии необходимо и достаточно, чтобы в диапазоне частот, где ЛАЧХ разомкнутой системы 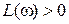, число переходов фазовой характеристической 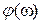прямой 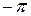снизу вверх (+) превышала на 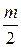число переходов сверху вниз (-), где m – число правых корней характеристического уравнения разомкнутой САР (рис. IV. 23).

В частном случае для устойчивой разомкнутой системы (m=0) необходимым и достаточными условием устойчивости замкнутой системы является следующее: в диапазоне частот, где 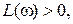фазовая частотная характеристика 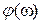не должна пересекать прямой 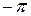или пересекать ее одинаковое число раз снизу вверх и сверху вниз (рис. IV. 24).

Заштрихованные области ЛАЧХ соответствуют .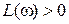

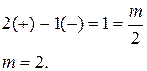
Если разомкнутая САР неустойчива и ее характеристическое уравнение имеет 2 правых корня, то при заданных ЛАЧХ и ЛФХ система в замкнутом состоянии устойчива.

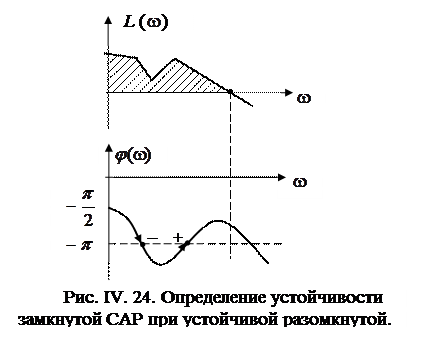
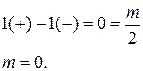
Итак, если правых корней нет (m=0), т.е. разомкнутая САР устойчива, то при заданных ЛАЧХ и ЛФЧХ система в замкнутом состоянии тоже устойчива.