IV. 3. 3. 3. Критерий Найквиста для разомкнутых систем, находящихся на границе устойчивости

В этом случае характеристическое уравнение разомкнутой системы имеет 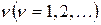нулевых корней, а сама система является астатической 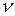-го порядка.

Передаточная функция такой системы выглядит следующим образом

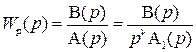. (IV. 3. 10)

Здесь характеристический полином 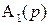имеет порядок 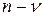, что обеспечивается равенством нулю последних 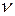коэффициентов полинома А(р):

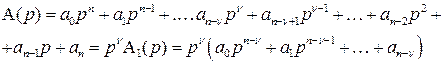
К примеру, для n = 5 при а₄ = а₅ = 0 т.е. 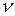= 2 получим

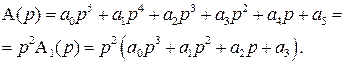для неустойчивой разомкнутой САР. оси.

е!)тельных и 1 системы.тельных преходов

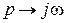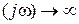Если в (IV. 3. 10) подставить , то из получившегося выражения можно усмотреть, что при АФХ разомкнутой системы W_p . Следовательно, критерий Найквиста, требующий, чтобы W_p 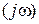начиналась на действительной оси, для разомкнутой системы, находящейся на границе устойчивости, в обычном, вышеприведенном, виде применять нельзя. Поэтому, (без доказательства) воспользуемся следующим приемом. АФХ разомкнутой САР W_p 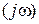дополним дугой бесконечно большого радиуса с угловым размером 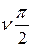(тем самым «сажая» начало W_p 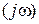на действительную ось) и уже к этой кривой применим критерий Найквиста. При этом следует иметь в виду, что определять устойчивость или неустойчивость разомкнутой САР надо будет по расположению корней относительно мнимой оси не характеристического уравнения А(р) = 0, как это было в IV. 3. 3. 1 и IV. 3. 3. 2, а уравнения А₁(р) = 0. Например, если уравнение А₁(р) = 0 имеет m правых корней, т.е. разомкнутая САР неустойчива, то в замкнутом состоянии САР будет устойчива, если при изменении частоты 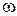от 0 до ∞ АФХ разомкнутой САР W_p 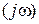, дополненная дугой 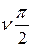бесконечно большого радиуса, охватывает точку (1; j0) в положительном направлении 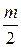раз.

Заметим, что и здесь критерий Найквиста можно применять в формулировке Я. З. Ципкина.

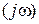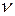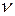На рис. IV. 19 приведены W_p трех различных систем с порядком астатизма =1, =2 и 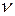=3. Пусть во всех трех случаях разомкнутые системы устойчивы, т.е. их характеристические уравнения А₁(р) = 0 содержат только левые корни.

Определим устойчивость этих систем в замкнутом состоянии.

Из рис. IV. 19 видно, что при 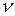=1 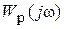с дополнительной дугой

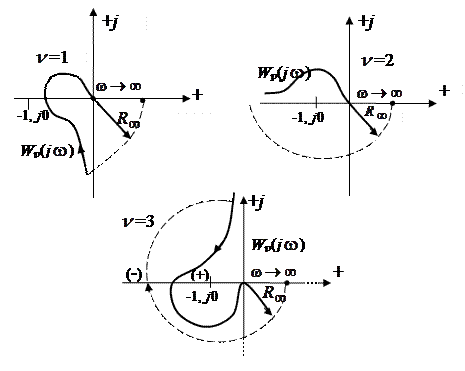
Рис. IV. 19. W_p , дополненные дугами бесконечно

большого радиуса для трех различных систем.

углового размера 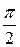, начинаясь на действительной оси, с ростом частоты не охватывает точку (1, j0). Следовательно, при устойчивой разомкнутой САР система в замкнутом состоянии устойчива.

При 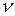=2 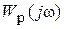с дополнительной дугой углового размера 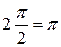и радиуса 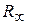охватывает точку (-1, j0), что приводит к неустойчивости системы в замкнутом состоянии.

При 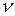=3 видно, что W_p 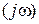с дополнительной дугой углового размера 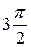и радиуса 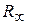имеет по Цыпкину одним положительной и один отрицательный переходы, это означает устойчивость замкнутой САР при устойчивой разомкнутой системе.