Определение устойчивости САР

П. IV. 1.

В замкнутой САР (рис. IV. 27) заданы (в числовом выражении)

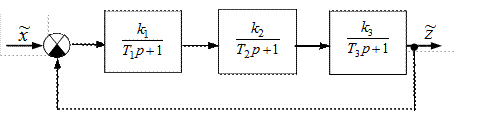
Рис. IV. 27. Функциональная схема замкнутой САР

все коэффициенты усиления k₁, k₂, k₃ и постоянные времени Т₁, Т₂, Т₃ инерционных звеньев.

Определить устойчивость разомкнутой и замкнутой САР и найти k_гр.

Решение.

Для решения поставленной задачи воспользуемся критерием Гурвица. Найдем передаточные функции, а затем и характеристические уравнения разомкнутой и замкнутой систем.

,

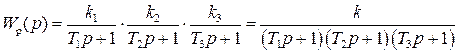где .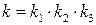

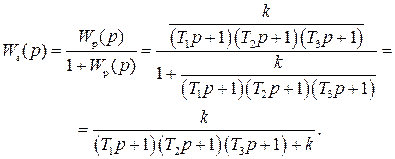
Для разомкнутой системы характеристическое уравнение имеет вид

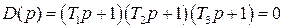(IV. 3. 11)

или

,

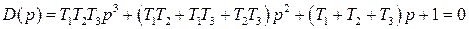а для замкнутой САР получается

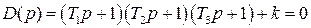(IV. 3. 12)

или

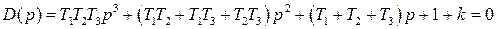. (IV. 3.13)

Нетрудно понять, что для исследования устойчивости разомкнутой САР применять критерий устойчивости Гурвица излишне, ибо непосредственно из вида характеристического уравнения разомкнутой системы (IV. 3. 11) легко найти, что все корни левые

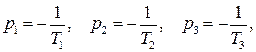
т. е. разомкнутая САР при всегда положительных Т₁, Т₂, Т₃ устойчива.

Вот по виду характеристического уравнения замкнутой САР (IV. 3. 12) так просто, как в предыдущем случае, определить соответствующие корни не удается, поэтому приходится применить критерий устойчивости Гурвица . При введении обозначений

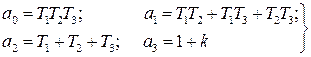(IV.3. 14)

характеристическое уравнение замкнутой САР (IV. 3. 13) примет вид

.

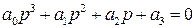В разделе IV. 2. 2 было выяснено, что для САР с характеристическим уравнением третьего порядка для устойчивости необходимо и достаточно при положительных коэффициентах a_i( i =0, 1, 2,3) выполнение условия ( IV. 2. 3)

.

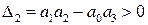Из (IV. 3. 14) видно, условия a_i>0 при положительных Т₁, Т₂, Т₃ и k всегда выполняются, а для проверки условия (IV. 2.3) надо в него подставить заданные значения параметров Т₁, Т₂, Т₃ и k и определить знак минора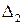

.

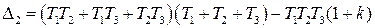Если этот минор больше нуля, то заданная замкнутая САР устойчива.

Граничный коэффициент усиления k_гр найдется из предпоследнего минора, приравненного к нулю

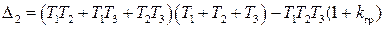=0.

Отсюда

.

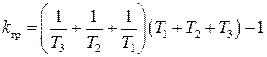Если, допустим, Т₁= Т₂ = Т₃ =Т , то

.

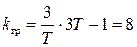П. IV. 2.

Характеристическое уравнение САР имеет вид

,

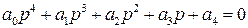где а₀=10 с⁴; а₁=5 с³; а₂=2 с²; а₃=10 с; а₄ = 0.

Определить устойчивость САР.

Решение.

Так как заданное характеристическое уравнение 4-го порядка имеет один неположительный коэффициент (а₄=0), то, согласно условию Стодолы (что в данном случае совпадает с критерием Гурвица) САР не сожжет быть устойчивой, а только либо нейтральной либо неустойчивой.

Запишем заданное характеристическое уравнение в другом виде

.

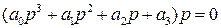Видно, что один из корней – нулевой. САР будет находиться на границе устойчивости, если все остальные корни характеристического уравнения левые (при наличии хотя бы одного правого корня САР будет неустойчивой). Эти остальные корни будут левыми, если выполняются условия устойчивости для уравнения

;

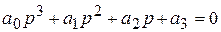а именно (согласно разделу IV. 2. 2)

а₀=10 с⁴ >0, а₁=5 с³ >0, а₂=2 с² >0, а₃=10 с >0 и

.

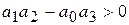После подстановки значений коэффициентов последнее неравенство

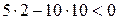
не выполняется, следовательно САР неустойчива.

П. IV. 3.

Передаточная функция разомкнутой САР имеет вид

,

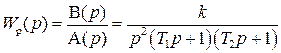причем k=50 c^-2, T₁=1 c, T₂=0.05 c.

Определить устойчивость замкнутой САР.

Решение.

Характеристическое уравнение замкнутой САР определяется выражением

,

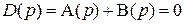или

.

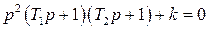После простого преобразования получим

.

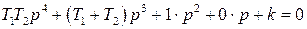Обозначим

.

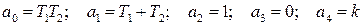Согласно критерию Гурвица для устойчивости системы необходимо, чтобы все a_i( i=0, 1, 2, 3, 4) > 0. В нашем же случае 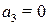, следовательно, замкнутая САР либо неустойчива, либо нейтральна. Для определения, в каком из этих двух состояний находится САР, воспользуемся достаточным условием Гурвица

.

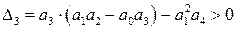Учитывая что 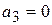, получим

.

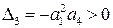Поскольку 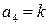>0 (коэффициент усиления k всегда больше нуля), минор 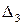никогда не может быть положительным. Значит, данная замкнутая САР всегда неустойчива (обычно говорят – структурно неустойчива), ибо никакими изменениями параметров САР k, Т₁, Т₂, оставаясь в области их положительных значений, нельзя систему сделать устойчивой. Для придания системе устойчивости надо менять ее структуру.

П. IV. 4.

Переходная функция разомкнутой САР имеет вид

,

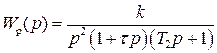где .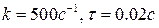

Определить постоянную времени Т_гр, при которой замкнутая САР находиться на границе устойчивости.

Решение.

Получим характеристическое уравнение замкнутой САР

.

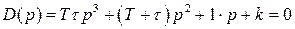Обозначим

.

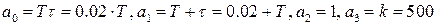Граница устойчивости определяется из равенства нулю второго минора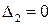

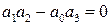
или

.

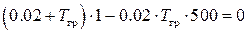Отсюда

.

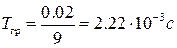П. IV. 5.

Характеристический полином САР 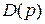имеет вид

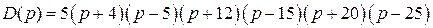
Каково изменение аргумента 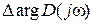при изменении частоты ?

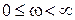Решение.

Характеристическое уравнение 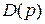= 0 имеет шесть корней (n=6), из них три правых (m=3). Поэтому, согласно принципу аргумента, получаем

.

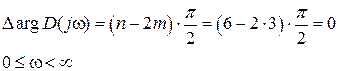П. IV. 6.

Какой из указанных годографов Михайлова замкнутой системы

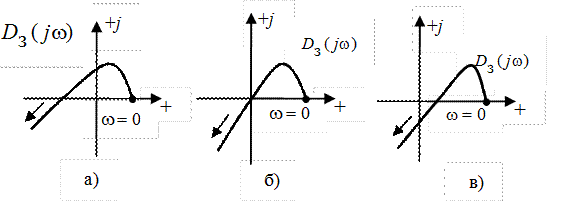
Рис. IV. 28. Годографы Михайлова для устойчивой, нейтральной и неустойчивой замкнутой систем.

соответствует САР с передаточной функцией

?

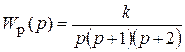Решение.

Характеристический полином замкнутой системы имеет вид

,

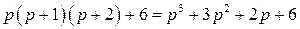т.е.

.

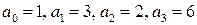Для этого полинома второй минор оказывается равный нулю

,

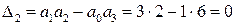т.е. замкнутая САР находится на границе устойчивости, что соответствует годографу Михайлова, имеющему вид рис. IV. 28, б.

П. IV. 7.

Возьмем снова пример П. IV. 1, положим в нем Т₁ = Т₂= Т₃ = Т и k₁ = k₂ = k₃ = k . Эти величины считаем заданными.

Определить устойчивость разомкнутой и замкнутой САР и найти k_гр.

Решение.

Запишем передаточные функции разомкнутой

,

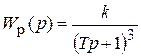а замкнутой САР

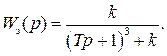
Поскольку из характеристического уравнения разомкнутой САР

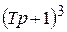=0,

следует, что все три его корня

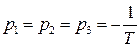
при положительном Т есть левые, то, значит, разомкнутая САР устойчива.

Для определения устойчивости замкнутой САР применим критерий Михайлова.

Характеристический полином замкнутой системы, имеющий третий порядок,

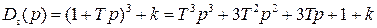
после замены 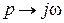примет вид

.

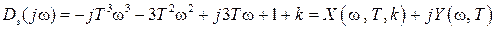В этом выражении мы выделили действительную часть 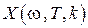и мнимую 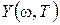части

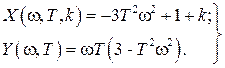(IV. 3. 15).

Ответ на вопрос – устойчива ли замкнутая САР можно получить по виду годографа Михайлова, зависящего от конкретных значений параметров k и T. Пусть для определенности k =5, T =1 с. Тогда соотношения (IV. 3. 15) примут

вид

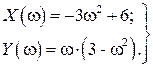
Задаваясь численными значениями от 0 до ∞, можно вычислить 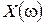и 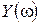для этих значений частоты , а затем построить годограф Михайлова .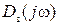

Таблица

			1.42	1.5	1.73		∞
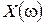
				-0.75	-3	-6	∞
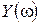
			1.42	1.125		-2	∞

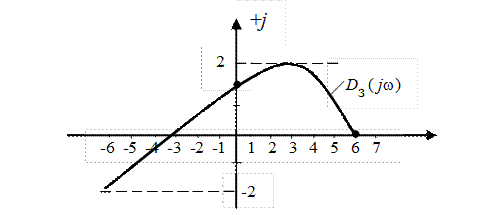
Рис. IV. 29. Годограф Михайлова.

Поскольку годограф Михайлова, начинается на положительном отрезке действительной оси, с ростом частоты от 0 до 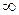последовательно в положительном направлении обходит все три квадранта (n=3), то для принятых k =5 и Т =1 с замкнутая САР устойчива.

Определим теперь k_гр. В разделе IV. 3. 2 было показано, что на границе устойчивости годограф Михайлова проходит через начало координат, т.е. выполняются условия (IV. 3. 4) .

В нашем случае при k = k_гр, 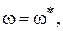Т =1 условия (IV. 3. 4) с учетом (IV. 3. 15) примут вид

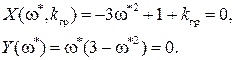
Из второго из этих уравнений, отбрасывая неверное решение 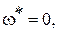при котором 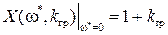(а должно быть для границы устойчивости равно нулю), получим

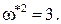
Подставляя это значение граничной частоты в выражение для 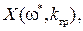получим

,

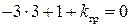т.е. k_гр = 8, как и в примере П. IV. 1.

П. IV. 8. Предыдущую задачу П. IV. 7. решить с помощью критерия Найквиста.

Решение.

Передаточную функцию разомкнутой системы мы получили в виде

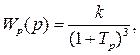
откуда ясно, что все корни характеристического уравнения левые и, значит, разомкнутая система устойчива.

Если провести замену 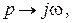то АФХ разомкнутой системы примет вид

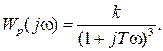
Построим эту характеристику. Найдем сначала 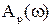и :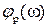

.

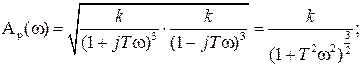
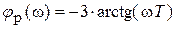При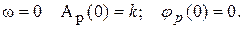

При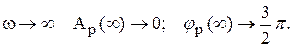

Следовательно, качественно АФХ разомкнутой системы W_p(j ) будет выглядеть следующим образом (рис. IV. 30).

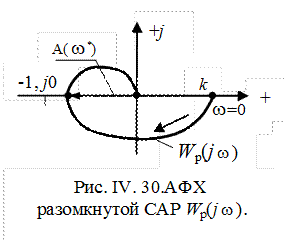
Устойчивость системы в замкнутом состоянии зависит от того, охватывает ли 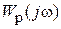критическую точку (-1, j ) или, иными словами, если A( ) > 1, то замкнутая САР неустойчива, при A( ) = 1 САР находится на границе устойчивости и приA( ) < 1 САР в замкнутом состоянии устойчива.

Найдем A( ). Для этого в первую очередь необходимо найти частоту ( ), при которой 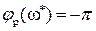. Получим

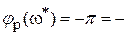3arctg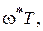

или

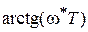
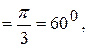
следовательно,

=

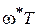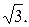
Поставим это значение в выражении для A_p( )

A_p( )= 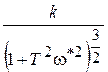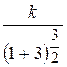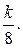_{= =} (IV. 3. 16)

Исследуем влияние коэффициента k на устойчивость замкнутой САР.

При k =5 A_p( ) = 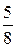< 1, значит САР устойчива,

при k =8 A_p( ) = 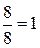, САР на границе устойчивости;

при k =16 A_p( 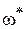) = 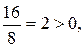САР неустойчива.

Из второго из этих заключений ясно, что k_гр = 8, тогда из (IV. 3. 16) получается формула для нахождения k_гр с помощью критерия Найквиста

k_гр= 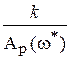. (IV. 3. 17)

Согласно этой формуле k_гр некоторой предложенной для исследования САР находится путем деления коэффициента усиления k этой САР на предварительно определенное значение A_p( ).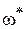

П. IV. 9.

С помощью критерия Найквиста определить, устойчива ли замкнутая САР, если в разомкнутом состоянии она описывает следующей операторной формой дифференциального уравнения

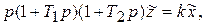
где k =100 c^-1, T₁=0.1 c, T₂=0.02 c. Каков k_гр?

Решение.

Из заданной операторной формы управления системы получим

W_p(j ) =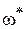

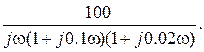
В отличии от предыдущего примера для разнообразия АФХ разомкнутой САР A_p( 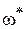) представим в декартовой форме

W_p(j )=

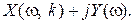
Для этого нужно освободиться от мнимости в знаменателе выражения для

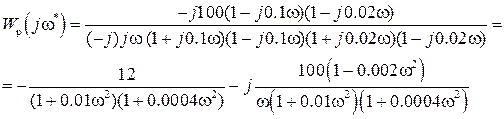(IV. 3. 18)

Определим величину 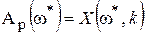. Понятно, что раз этот вектор расположен целиком на действительной оси, его мнимая часть равна нулю

.

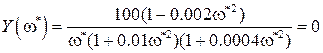Отсюда

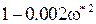= 0

и

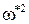=500 .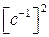

При подстановке этого значения частоты в X( , k) получим

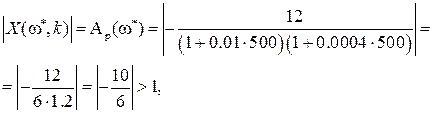
отсюда следует, что замкнутая САР неустойчива.

Найдем k_гр из (IV. 3. 17)

k_гр .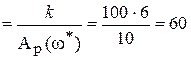

П. IV. 10. Предыдущий пример решить с помощью логарифмического критерия устойчивости.

Решение.

В предыдущем примере мы нашли, что АФХ разомкнутой системы имеет вид

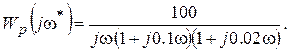
Получим отсюда выражение для АЧХ A_p( 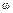) и ФЧХ 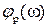разомкнутой системы

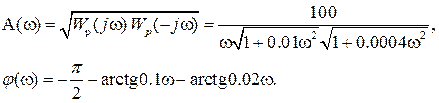(IV. 3. 19)

Имея в виду, что

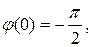
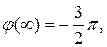
а сопрягающие частоты

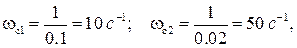
Построим асимптотическую ЛАЧХ и качественный вид ФЧХ разомкнутой системы.

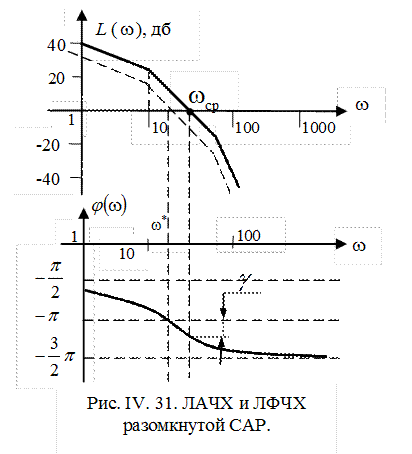
Найдем частоту среза 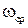. Из рис. IV. 31 видно, что ЛАЧХ пересекает ось частот на своем втором участке. Поэтому из выражения для точной ЛАЧХ

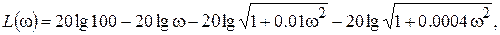
запишем выражение для ЛАЧХ на втором участке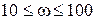

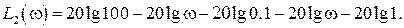
На частоте среза _ср эта асимптота будет равна нулю

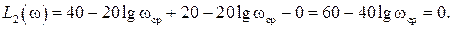
Отсюда

.

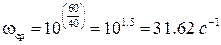Значение фазочастотной характеристики 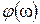(IV.3.19) при 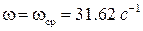будет

.

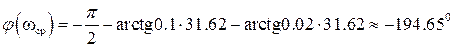Следовательно, запас устойчивости по фазе для данной системы будет отрицательным

,

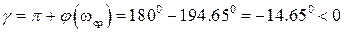а сама система в замкнутом состоянии неустойчива.

Граничный коэффициент усиления можно найти, исходя из того обстоятельства, что с изменением коэффициента усиления k ФЧХ системы не изменяется, а ЛАЧХ перемещается параллельно самой себе. На рис. IV. 31 показан случай границы устойчивости, когда при частоте 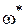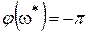, а ЛАЧХ при этой частоте (см. пунктир) пересекает ось абсцисс, т.е. А( 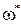)=1. отсюда и можно найти . Для этого найдем сначала частоту 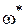, при которой .

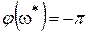Из (IV. 3. 19) получим

или

.

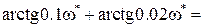
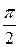Из тригонометрии известно, что

.

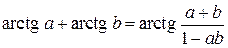В нашем случае

..

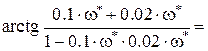
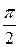Величине 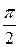арктангенс равен тогда, когда его аргумент бесконечен

,

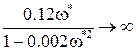а это для 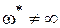возможно в случае, если

.

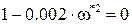Следовательно,

,

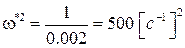а сама частота 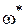=22.36 с^-1.

Величину найдем, приравняв нулю вторую асимптоту новой (пунктирной) ЛАЧХ

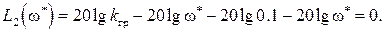
Подставим сюда =22.36 с^-1 и получим

.

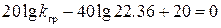Отсюда .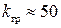

В предыдущем примере для той же задачи мы получили =60. Это объясняется тем, что в настоящем примере мы пользовались асимптотической (неточной ЛАЧХ), поэтому и здесь отличается от точного значения.

Вопросы для самопроверки.

1. Что понимается под устойчивостью системы?

2. Каковы признаки устойчивости САР?

3. Сформулируйте условие Стодолы.

4. Как найти граничное значение параметра по критерию устойчивости Гурвица.

5. Расскажите о принципе аргумента.

6. Что такое годограф Михайлова? Как он проходит в случае границы устойчивости системы?

7. Сформулируйте критерий устойчивости Найквиста для всех трех видов устойчивости разомкнутой САР.

8. Прокомментируйте связь логарифмического критерия устойчивости с критерием Найквиста.

9. Какие запасы устойчивости Вы знаете?