IV. 3. 3. 2. Критерий Найквиста для неустойчивых разомкнутых САР

Если разомкнутая САР неустойчива, то среди корней ее характеристического уравнения А(р) = 0 есть m 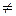0 правых корней. Тогда согласно принципу аргумента получим

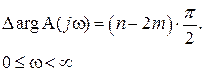
Чтобы замкнутая САР была устойчивой, надо чтобы ее характеристическое уравнение имело бы все корни левые. Тогда

.

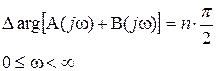В этом случае согласно (IV. 3.7) получим

.

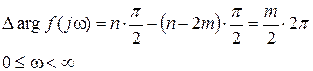Множитель 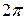обозначает, что вектор 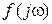совершает вокруг начала координат полный оборот.

Тогда критерий Найквиста для неустойчивых разомкнутых систем при учете (IV. 3. 9) может быть сформулирован следующим образом:

Для устойчивости замкнутой САР при неустойчивой разомкнутой системе необходимо и достаточно, чтобы АФХ разомкнутой САР W_p 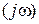, начинаясь на действительной оси, при росте частоты 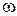от 0 до ∞ охватывала точку (-1, j0) в положительном направлении 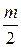раз, где m – число правых корней характеристического уравнения разомкнутой САР.

Пусть W_p 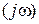имеет вид, изображенный на рис. IV. 16, и охватывает точку (-1, j0) в положительном направлении 1 раз, т.е. 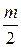= 1, поэтому m = 2.

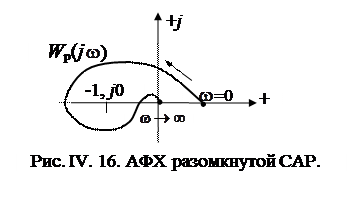
Это означает, что если характеристическое уравнение разомкнутой САР имеет 2 правых корня, система в замкнутом состоянии устойчива. Для W_p 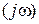, изображенной на рис. IV. 16, наличие у характеристического уравнения разомкнутой системы числа правых корней не равных 2, означает неустойчивость замкнутой САР.

Часто из-за наличия местных обратных связей АФХ разомкнутой САР совершает несколько оборотов вокруг точки (-1, j0) и имеет достаточно замкнутую конфигурацию (рис. IV. 17).

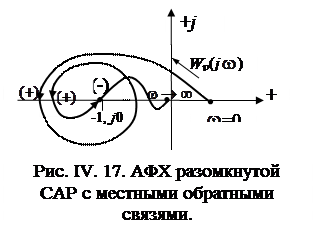
Здесь подсчитывать число оборотов W_p 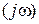вокруг точки (-1, j0) затруднительно. Для подобных случаев видный советский ученый Я. З. Цыпкин предложил удобную методику, базирующуюся на понятиях положительного и отрицательного переходов.

Переход амплитудно-фазовой характеристикой разомкнутой САР W_p 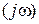с ростом частоты отрезка действительной оси 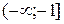сверху вниз называется положительным (+), а снизу в верх – отрицательным (–).

Тогда критерий Найквиста в формулировке Цыпкина предстает в следующем виде:

Замкнутая САР устойчива, если разность между числом положительных и отрицательных переходов равна 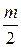, где m – число правых корней характеристического уравнения разомкнутой системы.

На рис. IV. 17 изображен случай, когда имеется два положительных и один отрицательный переход, т.е.

,

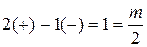и, значит, если характеристическое уравнение разомкнутой САР имеет 2 правых корня (только в этом случае!), замкнутая САР устойчива. Подчеркнем еще раз, что при подсчете переходов исследуется только участок 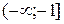и не принимается во внимание остальная часть действительной оси.

Сейчас мы рассмотрим случай IV. 3. 3. 2 для неустойчивой разомкнутой САР. Однако, вышеприведенная формулировка Цыпкина критерия Найквиста применима к случаю IV. 3. 3. 1, т. е. для устойчивой разомкнутой САР

(рис. IV. 18).

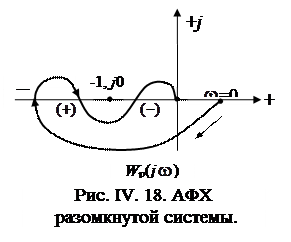
На этом рисунке изображена АФХ разомкнутой системы, имеющая 1 положительный и 1 отрицательный переходы. По Цыпкину

,

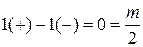таким образом, система будет устойчива, если разомкнутая система тоже устойчива, т.е. имеет m = 0 правых корней своего характеристического уравнения, а это и есть случай IV. 3.3.1.