IV. 3.1. Принцип аргумента

Пусть согласно (II. 7. 3)

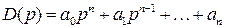
есть характеристический полином САР, согласно теореме Безу можно записать

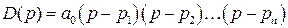где 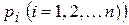– корни характеристического уравнения D(р)=0.

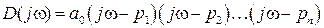Данное комплексное число имеет модуль

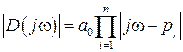
и аргумент

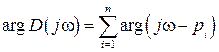Рассмотрим геометрическое представление комплексного числа ( 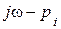) на плоскости Гаусса. Корень p_i на этой плоскости помечается точкой. В случае действительного корня эта точка расположена на вещественной оси, если имеется пара комплексно-сопряженных корней, то они располагаются симметрично относительно оси абсцисс.

На рис. IV. 8 корень p₁ отрицательный вещественный, корень p₂ – один из пары комплексно-сопряженных корней. Радиус-векторы, отвечающие этим числам, начинаются в начале координат и оканчиваются в точках p₁ и p₂.

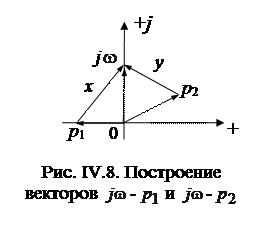
Радиус – вектор 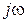, располагается целиком на мнимой оси. Его модуль определяется текущим значением частоты 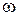. Так, при 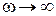вектор 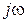уходит из начала координат вверх по оси ординат на бесконечно большое расстояние; при 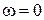вектор 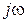совпадает с началом координат. По правилу геометрического сложения векторов

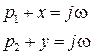Отсюда получаем искомые векторы x и y, дающие геометрическое представление комплексных чисел 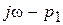и

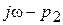
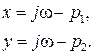
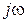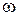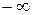В дальнейшем нас будет интересовать приращение аргумента вектора D( ) при изменении частоты от до 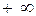, т.е.

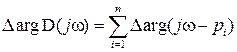(IV. 3.1.)

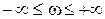
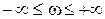
Здесь значок ∆ и обозначает изменение аргумента некоторого вектора при изменении частоты.

Эта величина зависит от того, в левой или правой полуплоскости располагаются корни характеристического уравнения .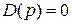

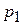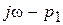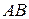Если, допустим, корень - «левый» (рис. IV. 9.), то вектор , при пройдет по линии вертикально вниз и в бесконечности пересечётся с мнимой осью, а при этот вектор будет направлен вертикально вверх и в бесконечности пересечется с осью абсцисс.

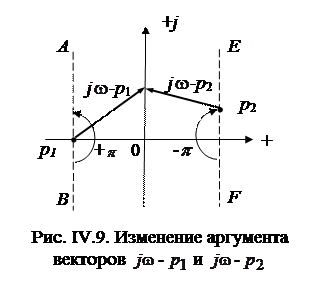
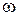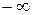Таким образом, при изменении частоты от до 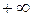вектор 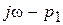повернется против часовой стрелки на угол 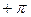и., следовательно,

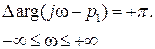
Если же 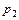- «правый» вещественный или один из пары «правых» коплексно-сопряженных корней, то при изменении частоты от 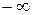до 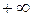вектор 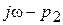повернется по часовой стрелке на угол 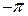, поэтому

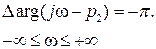
Если характеристическое уравнение 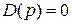имеет n корней, из которых m- «правых» (и, значит, n-m – «левых»), то, согласно (IV. 3.1.) получим

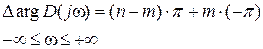Значит, изменение аргумента вектора 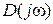при изменении частоты ω от до 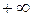равно разнице числа «левых» (n-m) и «правых» (m) корней, умноженной на 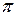. Это и есть принцип аргумента.

Перепишем последнее выражение для удобства в несколько ином виде

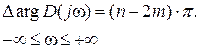
Выше было показано, что обычно частотные характеристики исследуются только для положительных частот, поэтому принцип аргумента будем записывать в виде

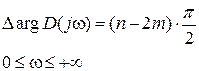, (IV. 3.2.)

то есть изменение аргумента вектора 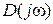при изменении частоты 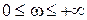равно разнице числа левых и правых корней, умноженной на .

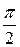IV. 3. 2. Критерий устойчивости А.Михайлова (1938)

Предлагаемый для изучения критерий устойчивости, опирающийся на принцип аргумента, может быть применен для исследования как разомкнутых так и замкнутых САР.

Пусть известен характеристический полином САР (неважно-разомкнутой или замкнутой)

.

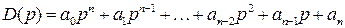При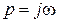

.

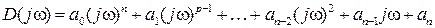В этом полиноме выделим действительную и мнимую части

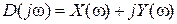, (IV. 3.3)

где

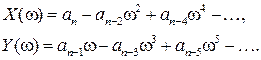
Если все коэффициенты 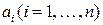заданы и задано определенное значение частоты ω = ω^*, то комплексная величина 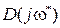изобразится на комплексной плоскости Гаусса в виде точки с координатам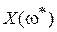и и 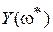или в виде вектора, соединяющего эту точку с началом координат. Если же значение частоты 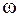менять непрерывно от нуля до бесконечности, то вектор 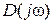будет изменяться по величине и направлению, описывая своим концом некоторую кривую, называемую годографом Михайлова.

Как было показано в разделе IV. 1, для устойчивости САР необходимо и достаточно, чтобы все корни характеристического уравнения системы были «левым», т.е. чтобы число «правых корней m = 0. В этом случае выражение для принципа аргумента (IV. 3. 2.) примет вид

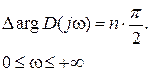
Отсюда становится понятной формулировкой критерия Михайлова.

Для устойчивости САР n-го порядка необходимо и достаточно, чтобы вектор 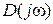при 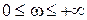, начинаясь на положительной части оси абсцисс, поворачивался с ростом частоты ω в положительном направлении на угол .

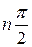В настоящее время обычно пользуются чуть видоизмененной формулировкой критерия, учитывая, что квадрантом называют одну четвертую часть плоскости Гаусса, охватываемую углом 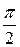(рис.IV.10) .

Для устойчивости САР n-го порядка необходимо и достаточно, чтобы годограф Михайлова, начинаясь на положительном отрезке действующей оси с ростом частоты от 0 до 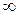проходят последовательно в положительном направлении n квадратов.

Годограф Михайлова для устойчивых систем всегда имеет плавную спиралевидную форму, причем конец ее уходят в бесконечность в том квадранте комплексной плоскости, номер которого равен степени характеристического уравнения n (рис. IV. 10.). Число квадрантов, больше чем n, годограф Михайлова вообще пройти не может.

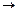На рис. IV.11. представлены годографы Михайлова для неустойчивых систем. Годографы а) и в) при росте частоты (направления роста частоты указывается стрелками) проходят квадранты в отрицательном направлении (по часовой стрелке), а у годографа с) нарушается последовательность прохождения квадрантов (I IV III вместо I II III).

Весьма важен случай нахождения САР на границе устойчивости (рис.IV.12.).

Рассмотрим положение годографа Михайлова в зависимости от какого-либо параметра САР, например коэффициента усиления k. Пусть при некотором k = k₁годограф занимает положение с), т.е. с ростом чистоты ω от 0 до ∞ он проходит квадраты I, IV, III. Выше мы установили, что этот случай отвечает случаю неустойчивости САР. Будем уменьшать коэффициент усиления, при этом, понятно, годограф Михайлова также будет изменяться. Допустим, при k = k₂ < k₁ годограф займет положение а), что соответствует устойчивости САР.

Нетрудно понять, что между этими положениями годографа а) и с) существует особое положение, когда эта кривая не подчиняется законам обхождения квадратов I→IV→III (неустойчивая САР) и I→II→III (устойчивая САР), а при некоторой частоте ω^* переходит через начало координат. Это и есть граница устойчивости системы с коэффициентом усиления k = k_гр.

Из факта, что на границе устойчивости годограф Михайлова проходит через начало координат, следует, что и действительная 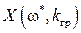и мнимая 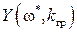части годографа равны нулю

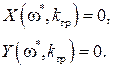(IV.3.4)

Из этих двух уравнений с двумя неизвестными можно найти ω^*и искомое k_гр.

IV. 3. 3. Критерий устойчивости Найквиста (1932 г.)

Этот критерий позволяет вынести суждение об устойчивости замкнутой системы с единичной отрицательной обратной связью по виду амплитудно-фазовой характеристики разомкнутой системы. Он (критерий) впервые был сформулирован в процессе исследования устойчивости электронных усилителей с отрицательной обратной связью.

Поскольку разомкнутая САР может быть устойчивой, неустойчивой и нейтральной (находящейся на границе устойчивости), различают три разновидности критерия Найквиста для устойчивых, неустойчивых и нейтральных разомкнутых САР.

Пусть передаточная функция разомкнутой САР имеет вид

,

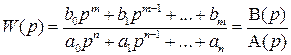причем, как уже отмечалось, m ≤ n (путь для определенности m< n).

Характеристическое уравнение разомкнутой САР n порядка имеет вид

А(р)=0.

Передаточная функция замкнутой САР с единичной обратной связью такова

.

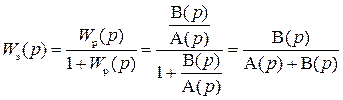Отметим здесь, что порядок характеристического уравнения замкнутой САР

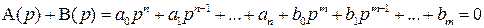
равен тоже n, т.к. порядок уравнения определяется наивысшей степенью переменной р, а, как договорились, m < n.

Образуем вспомогательную функцию

.

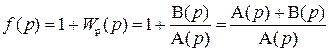Видно, что в знаменателе расположен характеристическиq полином n-го порядка разомкнутой САР, а в числителе – характеристический полином замкнутой САР того же порядка n.

При 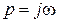получим на комплексной плоскости Гаусса радиус-вектор

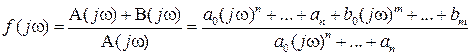. (IV.3. 5)

Из этого выражения ясно, что

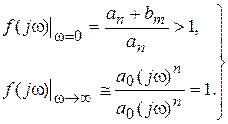(IV.3.6)

Нас будет интересовать изменение аргумента вектора 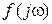при изменении частоты в диапазоне 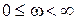. Из (IV.3.5) следует

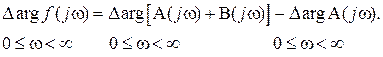(IV. 3. 7)

<56 7 8 9 10 11 >

Дата добавления: 2016-04-14; просмотров: 2109;