IV. 2. 1. Необходимые условия устойчивости А.Стодолы

Это условие предложено словацким профессором Стодолой, занимавшимся исследованием процесса регулирования турбин: система будет устойчивой, если все коэффициенты ее характеристического уравнения положительны.

Примечание. Заметим, что это условие можно сформулировать и по другому: все коэффициенты характеристического уравнения должны быть отрицательными, т.к. умножая характеристическое уравнение на минус единицу, можно сделать все коэффициенты положительными.

К сожалению, условие Стодолы является и необходимым и достаточным, если только порядок характеристического уравнения САР не превышает двух, т.е. при n =1 и n =2. Если же 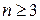, то условие Стодолы дает только необходимые условие, но не достаточные. К примеру, характеристическое уравнение второго порядка

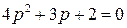
имеет все положительные коэффициенты, поэтому САР с таким уравнением устойчива.

САР с характеристическим уравнением 4-го порядка

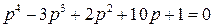
неустойчива, ибо не выполняются необходимые условия Стодолы (один коэффициент отрицателен). Если бы уравнение имело все положительные коэффициенты

,

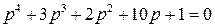то необходимое условие Стодолы выполнялось бы, но судить об устойчивости САР мы не могли бы, т.к. Стодола в этом случае не дает достаточных условий устойчивости. Решать подобные задачи мы научимся чуть позже, используя, скажем, критерии Гурвица.