Достаточный признак экстремума
| Пусть функция z = f (x, y) определена в некоторой окрестности стационарной точки М и имеет в этой точке непрерывные частные производные второго порядка, равные А, В и С. Тогда, если определитель Δ = АВ – С2 > 0, то в данной стационарной точке М функция z = f (x, y) имеет экстремум, причем, если A < 0, то максимум, если A > 0, то минимум. Если Δ < 0, то в точке М экстремума нет. |
Замечание. Если в стационарной точке М: Δ = АВ – С2 = 0, то наличие экстремума возможно, но для этого требуется проведение дополнительных исследований.
ПРИМЕР: Найти экстремумы функции 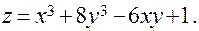
Вычислим частные производные первого и второго порядка данной функции:
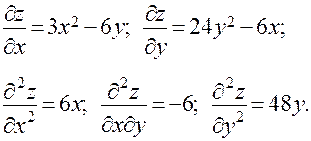
Для нахождения стационарных точек приравняем к нулю частные производные первого порядка и получим систему уравнений:
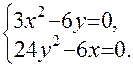 или:
или: 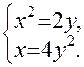
Решая эту систему, получим две стационарные точки М(0, 0) и N(1, 1/2).
Для выяснения наличия экстремумов и их характеров в этих точках вычислим значения частных производных второго порядка последовательно в каждой точке.
Для стационарной точки М(0, 0) получим:
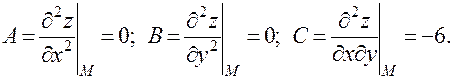
Поскольку: Δ = АВ – С2 = - 36 < 0, в этой стационарной точке экстремума нет.
Для стационарной точки N(1, 1/2) получим:
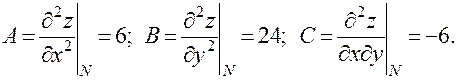
Поскольку Δ = АВ – С2 = 108 > 0 и A = 6 > 0, заключаем, что в этой стационарной точке будет локальный минимум данной функции. Причем значение функции в точке минимума будет равно 0.
Дата добавления: 2016-04-11; просмотров: 1527;
