Достаточный признак сходимости знакопеременного ряда
| Если ряд, составленный из модулей членов знакопеременного ряда, сходится, то сходится и исходный знакопеременный ряд. |
Ряд называется абсолютно сходящимся, если сходится сам ряд, так и ряд, составленный из модулей его членов.
Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из модулей его членов, расходится.
ПРИМЕР: Ряд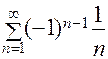 
является условно сходящимся, поскольку сам этот ряд сходится по признаку Лейбница (убедитесь в этом сами), а ряд, составленный из модулей его членов 
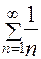, расходится как гармонический ряд.
Степенные ряды
Степенным рядом называется ряд, имеющий вид:
.
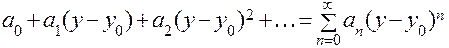Где an – действительные числа, а число y0 называется центром степенного ряда.
Замена x = y – y0 переводит степенной ряд к новому виду, который называется степенным рядом с нулевым центром:
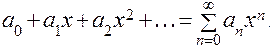
ПРИМЕР: Ряд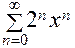 
является степенным рядом с нулевым центром.
Совокупность значений х, при которых степенной ряд с нулевым центром сходится, называется областью сходимости степенного ряда.
Структура области сходимости степенного ряда устанавливается следующей теоремой.
Теорема Абеля
| Если степенной ряд сходится при x = x0 ¹ 0, то он сходится и притом абсолютно, при всех х таких, что ½х½< ½x0½. Если степенной ряд расходится при х = х1, то он расходится при всех х таких, что ½х½> ½x1½. |
Радиусом сходимости степенного ряда с нулевым центром называется число R ³ 0 такое, что при ½х½< R ряд сходится, а при ½х½> R ряд расходится. При этом интервал (- R, R) называется интервалом сходимости степенного ряда.
Замечание.На концах интервала сходимости, т.е. при х = ± R, ряд может как сходиться так и расходиться.
Радиус сходимости степенного ряда определяется формулой:
|
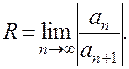
ПРИМЕРЫ:
1. Для степенного ряда 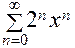найдем: 
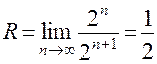. Поэтому данный ряд сходится на интервале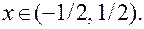 
2. Для степенного ряда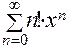 
найдем: 
. Поэтому данный ряд сходится только в одной точке х = 0.
Специфическими разновидностями конечных степенных рядов являются ряды Тейлора и Маклорена.
Пусть функция f (x) имеет в точке а и в некоторой ее окрестности производные порядка до (n + 1) включительно, а х – любое значение аргумента из указанной окрестности и х ¹ а. Тогда существует точка q Î (а, х) такая, что справедлива формула:
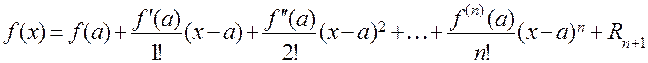
Эта формула называется формулой Тейлора, а представление функции в виде степенного ряда называется разложением функции в ряд Тейлора. Последнее слагаемое в формуле Тейлора
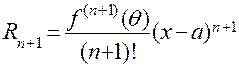
называется остаточным членом и характеризует абсолютную погрешность представления функции в виде ряда Тейлора с n слагаемыми.
Если в формуле Тейлора положить а = 0, то получим формулу Маклорена:
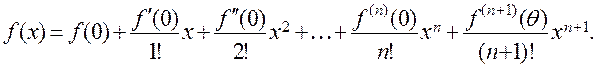
Представление функции в виде степенного ряда по формуле Маклорена называется разложением функции в ряд Маклорена.
Обе приведенные формулы позволяют с контролируемой точностью заменять любые дифференцируемые функции многочленами (конечными степенными рядами) в некоторой, небольшой, окрестности либо точки а (ряд Тейлора), либо точки 0 (ряд Маклорена).
ПРИМЕР: Разложить функцию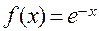 
в ряд Маклорена.
Поскольку все производные нечетного порядка заданной функции имеют вид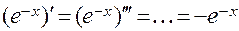 
и, следовательно, при х = 0 равны (- 1), а все производные четного порядка при х = 0 равны 1, можно заданную функцию представить в виде:
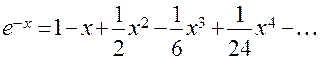
Дата добавления: 2016-04-11; просмотров: 904;