Приближенное вычисление определенных интегралов
Выше уже упоминалось о том, что достаточно мощным средством вычисления определенных интегралов является формула Ньютона-Лейбница. Однако ее практическое применение бывает связанным с существенными трудностями, возникающими при достаточно сложном аналитическом виде подынтегральной функции. С другой стороны, эта формула оказывается вообще неприменимой, когда речь идет о функциях, первообразные которых не выражаются в элементарных функциях. В этих и некоторых других случаях часто используют численные методы, позволяющие найти приближенное значение искомого определенного интеграла с требуемой точностью.
Существуют различные численные методы или формулы приближенного вычисления определенных интегралов. Ниже рассматривается наиболее распространенная из них – формула трапеций.
Пусть на отрезке [a, b] задана непрерывная и неотрицательная функция y = f (x). Мы уже знаем, что определенный интеграл от этой функции по отрезку [a, b] численно равен площади под кривой ее графика на этом отрезке. Очевидно, что мы получим приближенное значение искомого интеграла, если вместо площади под кривой возьмем площадь под ломаной, расположенной достаточно близко к исходной кривой. Для построения этой ломаной разобьем отрезок [a, b] на n равных частей длиной h = (b – a)/n каждая, и на каждом из полученных отрезков разбиения заменим участок кривой хордой, стягивающей концевые точки (рис. 18).
Тогда можно записать следующее приближенное равенство:
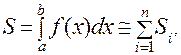
где Si – площадисоответствующих трапеций, каждая из которых равна: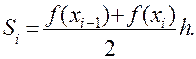 
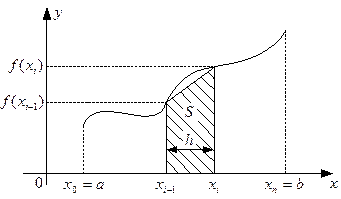
Рис. 18
Поэтому будет справедливо следующее равенство:
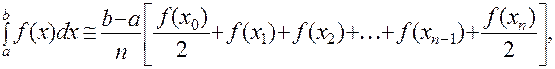
где: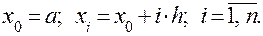 
Полученная в итоге формула и носит название формулы трапеций.
Доказано, что абсолютная погрешность D результата вычислений по формуле трапеций, т.е. величина разности между этим и истинным значением интеграла, может быть оценена по формуле:
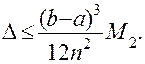
где: (b - a) – длина отрезка интегрирования, n – количество отрезков разбиения, М2 – максимальное значение модуля второй производной подынтегральной функции на отрезке [a, b].
ПРИМЕР: Пользуясь формулой трапеций, найти приближенное значение интеграла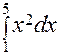 
и сравнить результат с точным значением.
Разобьем отрезок [1, 5] на 10 равных отрезков, длиной 0,4 каждый. Вычислим значения функции в точках разбиения:
| xi | 1,4 | 1,8 | 2,2 | 2,6 | 3,0 | 3,4 | 3,8 | 4,2 | 4,6 | 5,0 | |
| yi | 1,96 | 3,24 | 4,84 | 6,76 | 9,0 | 11,56 | 14,44 | 17,64 | 21,16 | 25,0 |
По формуле трапеций имеем: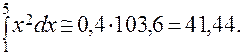 
Точное значение этого интеграла (убедитесь в этом сами) равно 124/3, следовательно, абсолютная погрешность нашего приближенного вычисления будет равна:
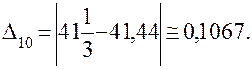
С другой стороны эту же погрешность можно оценить по приведенной выше формуле, в которой М2 = 2, т.к. f″(x) = 2:
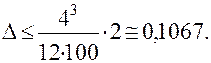
Дата добавления: 2016-04-11; просмотров: 1117;