Вычисление количественной оценки статистической связи между качественными показателями деятельности фирм
Для оценки наличия и тесноты связи между двумя объектами, свойства которых описываются качественными показателями, используют метод ранжирования, присваивая показателям каждого объекта ранг от 1 до n в порядке, соответствующему ухудшению свойств, и вычисляют коэффициент ранговой корреляции.
Результат такой процедуры может найти применение в случае сравнительной оценки как деятельности фирм, так и производимой ими продукции при сопоставлении ее с более совершенной. Это позволит своевременно скорректировать план маркетинга в части повышения качества и установления оптимальной цены на товар.
Пример 1. В табл. 4 приведена оценка имиджа основных пивоваренных предприятий (ОАО «Ярпиво» и ОАО «Балтика») по девяти показателям на рынке Ярославской области по пятибалльной шкале [14]. Требуется оценить связь между показателями фирм «Ярпиво» и «Балтика», присвоив ранги соответствующим баллам (столбцы 3 и 5), с помощью выборочного коэффициента ранговой корреляции Спирмена.
Таблица 4
Сравнительная характеристика предприятий по основным показателям
| Показатели (высказывания потребителей) | ОАО «Ярпиво» | ОАО «Балтика» | ||
| Оценка | Ранг (X) | Оценка | Ранг (Y) | |
| Хорошо известная компания | 4,9 | 4,9 | ||
| Компания с большим будущим | 4,7 | 4,8 | ||
| Компания, способная противопоставить свою продукцию конкурентам | 4,5 | 4,6 | ||
| Быстрорастущая компания | 4,4 | 4,6 | ||
| Компания, вызывающая доверие | 4,3 | 4,5 | ||
| Компания, заботящаяся о потребителе своей продукции | 4,2 | 4,3 | ||
| Компания, заботящаяся о качестве своей продукции | 4,1 | 4,3 | ||
| Фирма, проводящая хорошо рекламную кампанию | 4,0 | 3,9 | ||
| Компания, проводящая правильную ценовую политику | 4,0 | 3,5 |
Решение. Для вычисления коэффициента ранговой корреляции определяют разности рангов по каждому показателю:
di = xi – yi.
d1 = 1 – 1 = 0; d2 = 2 – 2 = 0; d3 = 3 – 3 = 0; d4 = 4 – 3 = 1;
d5 = 5 – 4 = 1; d6 = 6 – 5 = 1; d7= 7 – 5 = 2; d8 = 8 – 6 = 2; d9 = 8 – 7 = 1.
Сумма квадратов разностей рангов
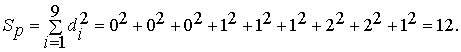
Значение коэффициента ранговой корреляции при числе объектов, равном n = 9:
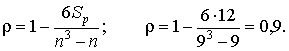
Существенность коэффициента корреляции проверяется с помощью t-критерия Стьюдента, затем исследуется гипотеза о равенстве нулю коэффициента ранговой корреляции для генеральных совокупностей Н0: ρ = 0 при конкурирующей Н1: ρ≠ 0. При | ρ | > Tкр нулевая гипотеза отвергается. Величина критической точки вычисляется по формуле
Ткр = tкр(a; k)[(1 – ρ2)/(n – 2)]0,5, (1.14)
где a – уровень значимости, a = 0,1; k – число степеней свободы,
k = n – 2; n – объем выборки.
По табл. 7 приложения для двусторонней критической области определяется значение tкр(0,1; 7) = 1,8946, тогда
Ткр = 1,8946[(1 – 0,92)/(9 – 2)]0,5 = 0,31.
Поскольку | ρ | > Ткр, нулевая гипотеза отвергается, коэффициент ранговой корреляции ρ = 0,9 значим.
Пример 2. По данным табл. 4, записанным в виде табл. 5, рангов требуется оценить связь между показателями деятельности фирм с помощью коэффициента ранговой корреляции Кендалла.
Таблица 5
Ранговые оценки показателей деятельности ОАО «Ярпиво» и «Балтика»
| ОАО «Ярпиво», xi | |||||||||
| ОАО «Балтика» yi |
Решение. Правее у1 находятся 8 рангов, больших, чем у1(2, 3, 3, 4, 5, 5, 6, 7), поэтому R1 = 8. Правее у2 – 7 рангов (3, 3, 4, 5, 5, 6, 7), поэтому R2 = 7 и далее: R3 = 5; R4 = 5; R5 = 4; R6 = 2; R7 = 2; R8 =1. Сумма рангов R = 34.
Коэффициент ранговой корреляции Кендалла при n = 9
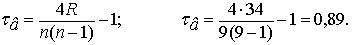
Значимость коэффициента τв оценивается также с помощью t-критерия. Проверяется нулевая гипотеза о равенстве нулю генерального коэффициента ранговой корреляции Н0: ρг = 0 при конкурирующей Н1: ρг ≠ 0.
Значение, соответствующее критической точке, вычисляется по формуле
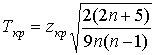 , (1.15)
, (1.15)
где zкр – критическая точка двусторонней критической области, отвечающая равенству Ф(zкр) = (1 – a)/2; n – объем выборки.
При |τв| > Ткр нулевая гипотеза отвергается.
Для вычисления Ткр вначале с помощью функции Лапласа (табл. 8 приложения) при уровне значимости a = 0,1 определяется критическая точка zкр из соотношения
Ф(zкр) = (1 – a)/2 = (1 – 0,1)/2 = 0,45, откуда zкр = 1,645, тогда
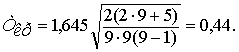
Поскольку |τв| > Ткр, нуль-гипотеза отвергается, согласно альтернативной гипотезе Н1 выборочный коэффициент ранговой корреляции Кендалла так же как и коэффициент, найденный по способу Спирмена, значим. Тот факт, что они несколько разнятся между собой, неважен, так как область возможных значений случайной величины ρ охватывает значение τв, являющегося также случайной величиной.
По результатам расчета можно сказать, что и той, и другой компании следует внимательно отнестись к пункту о проведении правильной ценовой политики, а фирме «Ярпиво» обратить внимание еще и на повышение качества своей продукции: при однородности всех остальных показателей качество продукции фирмы «Ярпиво» резко снизило коэффициент ранговой корреляции между показателями фирм. Характер других оценок показывает, что обе фирмы находятся на подъеме, но вся их деятельность направлена только на агрессивный захват рынка любой ценой, включая здоровье покупателей, и потребителю следовало бы обходить стороной их продукцию.
Дата добавления: 2016-03-27; просмотров: 849;
