B1nсоставляющейи вектором B1 индукции магнитного поля в среде магнетикаμ1 магнитной проницаемостью, а также α2 угол между нормальной B2nсоставляющейи вектором

B₂ индукциимагнитного поляв среде магнетикас μ₂ магнитной проницаемостьюсвязаны между собой следующим соотношением: tqα₁/tqα₂ = (B_1τ/B_1n)/(B_2τ/B_2n)= μ₁/μ₂, (7.134)

где для рис.7. 29 μ₁ >μ₂.

Магнитное поле проводника с током в вакууме и при заполнении пространства, окружающего его, однородным непроводящим магнетиком

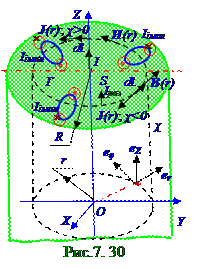
В магнитном поле проводника с током в вакууме векторы B(r) индукции (7.6) из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях", H(r) напряжённости(7.120), намагниченности J(r) (7.126) магнитного поля представляют собой цилиндрическое векторное поле, поскольку все эти векторы(рис.7.30) находятся на окружностях, соосных с цилиндрическимпроводником из магнетикас χ магнитной восприимчивостью, и направленыпо касательнойк этой окружности, т.е. коллинеарны e_φ орту цилиндрической системыкоординат.

Циркуляция (7.122) вектора H(r)напряжённостимагнитного поля в интегральномвиде повоображаемой окружности(рис.7.30) радиусом rв области пространства, занятого магнетиком, равнарезультирующему I_рез макроскопическому или току проводимости через поверхность S площадью, которую охватывает эта окружностьr радиусом. Охватываемая воображаемой окружностьюr радиусом поверхность - это кругr радиусом от поперечного сечения цилиндрического проводника, перпендикулярного его оси. По нормалик поверхности этого круга(рис.7. 30)течётток проводимости с j А/м² модулём jвектораплотности, который имеет следующий вид: j = I/πR² А/м². (7.135)

∫Hdl = H_l2πr = I_рез ↔ H_l = I_рез/2πr↔ H = I_рез/2πr, (7.137) Г

где (рис.7. 30) 0 ≤ r ≤ R.

Поперечное сечение цилиндрическогопроводникаиз магнетика c χ магнитной восприимчивостью (рис.7.30) перпендикулярно его оси, поэтому вектор dl обхода Г контура r радиусом тоже перпендикулярен оси цилиндрическогопроводника и сонаправлен e_φ орту в цилиндрической системекоординат. С учётом сонаправленности e_φ орта вектору dl обхода Г контура r радиусомH_l проекция навектор dl обхода Г контураравна H_φ проекции вектора H напряжённостимагнитного поляна e_φ орт, т.е. H_l= H_φи она положительна при положительном направлении обхода Г контура r радиусомпротив "часовой стрелки" и направлении результирующего I_рез макроскопического или тока проводимости по OZ оси,поэтомус учётом равенстванулюпроекцийH _r, H _Z вектора H напряжённостимагнитного поляна соответственно e_r, e_Z орты в цилиндрической системекоординат эта H_l проекция равна H модулю (7.137) вектора H напряжённостимагнитного поля.

Вектор J намагниченностиJ (7.126) магнетика, из которой изготовленцилиндрическийпроводник, имеет следующий вид: J = χH,(7.138)

где вектор J намагниченности магнетика (рис.7.30) сонаправлен вектору H напряжённостимагнитного поля (7.138)в магнетике цилиндрическогопроводника, когда χ > 0 для парамагнетикови ферромагнетиков, и вектор J намагниченности противонаправлен вектору H напряжённостимагнитного поля в магнетике цилиндрическогопроводника, когда χ < 0 для диамагнетиков. Подставляем магнитную χ восприимчивость магнетика, из которой изготовленцилиндрическийпроводник, а также H_l проекцию наdl вектор, которая равна H модулю (7.138) вектора H напряжённостимагнитного поля, в (7.137), и получаем следующее выражение для J _l(r) проекции навектор dl обхода Г контура вектора J намагниченности магнетика, из которой изготовленэтот цилиндрическийпроводник,в функции от r радиуса (рис.7.31) окружности, охватывающей круговуюповерхность магнетика S площадью: J _l = χH = χrI/2πR² А/м,(7.139)

где (рис.7. 30) 0 ≤ r ≤ R.

Проекция J _l(r) навектор dl обхода Г контура (7.137) вектора J намагниченности магнетика(рис.7.30),в функции от r радиуса окружности, охватывающей круговуюповерхность магнетика S площадью, является положительнойвеличиной, когда χ > 0 для парамагнетикови ферромагнетиков, и является отрицательнойвеличиной, когда χ < 0 для диамагнетиков.

Проекция J _l(r) навектор dl обхода Г контура вектора J намагниченности магнетика(рис.7.30) на круговойповерхности магнетикасr = R радиусом с учётом(7.139) имеет следующий вид: J _{l|r = R} = χI/2πR А/м. (7.140) Вектор J(r) намагниченностимагнетика(рис.7. 30) коллинеарен e_φ орту цилиндрической системыкоординат, поэтому векторное выражение (7.138) имеет следующий вид: J = χH = e_φ χrI/2πR² А/м,(7.141)

где (рис.7. 30) 0 ≤ r ≤ R и вектор J(r) намагниченности магнетика сонаправлен вектору H напряжённостимагнитного поля, если χ>0 для парамагнетикови ферромагнетиков, и противонаправлен вектору H напряжённостимагнитного поля в магнетике цилиндрическогопроводника, когда χ < 0 для диамагнетиков.

Ротация вектора J(r) намагниченности (7.141) магнетикас учётом равенства нулю проекцийJ_r, J_Z этоговектора на соответственно e_r, e_Z орты в цилиндрическойсистемекоординат и отличия от нуляпроекцииJ_φ(r) на e_φ орт, а также с учётом зависимости этой проекции J_φ только от r модуля r радиуса-вектора, направленного по орту e_r, и равенства проекцииJ_φ(r) на e_φ орт проекции J _l(r) навектор dl обхода Г контура вектора J намагниченности магнетика(рис.7.30), т.е. J_φ(r)= J_l(r) приводит к следующему выражению вектора j_мол плотности молекулярных токов (7.116), равным значениюротора намагниченности [J] в произвольной точке пространства, зависящей в цилиндрическойсистемекоординат только от r модуля r радиуса-вектора:

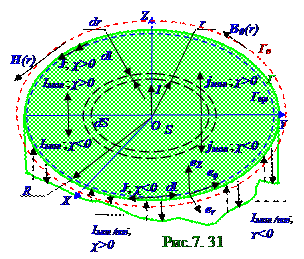
j_мол = [ J] ={(1/r)[∂(rJ_φ)/∂r]}e_Z =e_ZχI/πR²,(7.142) где (рис. 7.31) 0 ≤ r ≤ R.

Вектор j_мол плотности молекулярных токов магнетиканаправлен (рис.7.31) по e_Z орту в цилиндрическойсистеме координат, т.е. в одну сторону срезультирующейтоком I силойпроводимости в магнетике цилиндрическогопроводника, если χ>0 для парамагнетикови ферромагнетиков, а, если χ < 0 для диамагнетиков, то вектор j_молплотности молекулярных токов магнетиканаправлен противоположно e_Z орту в цилиндрической системе координат, т.е. в противоположную сторону срезультирующейтоком I силойпроводимости в магнетике цилиндрическогопроводника.

Проекция j_молZ наe_Z орт в цилиндрической системекоординат (рис.7. 31) вектора j_мол плотностимолекулярных токов имеет следующий вид с учётом её (7.142) постоянной величины в пределах поперечного сечения кругаR радиусоммагнетика цилиндрическогопроводника:j_молZ = χI/πR²,(7.143)

где (рис.7.31) 0 ≤ r ≤ R.

Проекция j_молZ является положительнойвеличиной, если χ>0 для парамагнетикови ферромагнетиков, а, если χ < 0 для диамагнетиков, то проекция j_молZ является отрицательнойвеличиной.

Молекулярныйток dI_мол силой (7.108) ток, текущий через кольцо с элементарной(рис.7. 31) толщиной dr и r радиусом, который находится в интервале 0 ≤ r ≤ R значений, с учётом её (7.143) имеет следующий вид: dI_мол = j_молZ 2πrdr = (χI/πR²)2πrdr = χ2Irdr/R², (7.144)

где dS = 2πrdr - площадь элементарногокольца в поперечном сечении цилиндрического проводника, перпендикулярного его оси; перпендикулярноповерхностиэтогоэлементарногокольца течёт молекулярныйток dI_мол силой.

МолекулярныйI_молток, текущий (рис.7.31) через поперечное сечение кругаR радиусоммагнетика цилиндрическогопроводника, перпендикулярного его оси, с учётом (7.143) , согласно (7.144), имеет следующий вид: R R I_мол = ∫j_молdS= ∫ dI_мол = (χ2I/R²) ∫rdr = χI А, (7.145)

S 0 0

где молекулярныйI_молток направлен по e_Z орту в цилиндрической системе координат, т.е. в одну сторону стоком Iсилойпроводимости в магнетике цилиндрическогопроводника, если χ>0 для парамагнетикови ферромагнетиков, а, если χ < 0 для диамагнетиков, то молекулярныйI_мол результирующийтокнаправлен противоположно e_Z орту в цилиндрической системе координат, т.е. в противоположную сторону стоком Iсилой проводимости в магнетике цилиндрическогопроводника.

Молекулярныйток I_мол силой согласно (7.115) определяется циркуляцией вектора J_прнамагниченностиповоображаемой окружности(рис.7.31) r= R радиусом Г_пр контуру c внутреннейстороны поперечного сечения цилиндрическогопроводникаиз магнетика c χ_пр магнитной восприимчивостью, перпендикулярного его оси. С учётом (7.139) проекции J_{пр l} навектор dl обхода Г_пр контура вектора J_прнамагниченности магнетика(рис.7.31) на круговойповерхности магнетикасr = R радиусом, т.е. Г_пр контуре, который охватывает поперечное сечениемагнетикаэтогоцилиндрическогопроводника,молекулярныйток I_мол силой, текущий через поперечное сечение магнетика R радиусомS = πR² площадьюцилиндрическогопроводника, перпендикулярное его оси,имеет следующий вид:

I_мол = ∫J_прdl= ∫J_{пр|r =R} dl= J_{прl|r = R}2πR = (χI/2πR) 2πR = χI А,(7.146) Г_пр Г_{пр|r = R}

где молекулярныйI_мол результирующий(рис.7.31) ток направлен по e_Z орту в цилиндрической системе координат в одну сторону стоком Iсилойпроводимости в магнетике цилиндрическогопроводника, если χ>0 для парамагнетикови ферромагнетиков, т.е. когда J_пр вектор намагниченности сонаправленвектору dl обхода Г_пр контура R радиусом и поэтому J_прl проекция этого вектора J_пр намагниченностинавектор dl обхода Г_пр контура является положительнойвеличиной; молекулярныйI_мол результирующий(рис.7.31) ток направлен противоположно e_Z орту в цилиндрической системе координат и току Iсилойпроводимости в магнетике цилиндрическогопроводника, если χ < 0 для диамагнетиков, т.е. когда вектор J_пр намагниченности противонаправленвектору dl обхода Г_пр контура R радиусом и поэтому J_прl проекция этого вектора J_пр намагниченностинавектор dlобхода Г_пр контура является отрицательнойвеличиной.

Равенство(7.145) и (7.146) соответствует следующему выражению (7.115): I_мол = ∫j_молdS = ∫Jdl, (7.147) S Г

что является подтверждением правильности расчётов в данном выводе.

Циркуляция (7.146) вектора J_в(r) намагниченности (7.141) магнитного поля повоображаемой окружности -(рис.7. 31) Г_в контуру R радиусом c внешнейстороны поперечного сечения(рис.7.31) магнетика цилиндрическогопроводника, перпендикулярного его оси, равнаследующей сумме молекулярныхтоков I_мол;I_{мол.пов.}силой,соответственно текущих перпендикулярно поверхности S площадью этого поперечного сечения и по боковой поверхности цилиндрическогопроводникаиз магнетика:

где (7.148) приравнено нулю, п.ч. Г_в контур R радиусом c внешнейстороны поперечного сечения цилиндрического проводникаиз магнетикапроходит в вакууме,где векторJ_в(r) намагниченностиравен нулю.

которую охватывает эта окружностьr радиусом: ∫Hdl = H_l2πr = I ↔ H_l = I/2πr↔ H = I/2πr, (7.149) Г_м

где (рис. 7. 32) 0 ≤ r ≤ R; I - сила макроскопического или тока проводимости, текущего перпендикулярно поверхности S = πR² площадью, которая представляет собой поперечное сечение цилиндрического проводникаиз магнетика с χ_пр магнитной восприимчивостью.

Поперечное сечение цилиндрическогопроводникаиз магнетика c χ_пр магнитной восприимчивостью (рис.7.32) перпендикулярно его оси, поэтому вектор dl обхода Г_м контура c внешнейстороны этого поперечного сечения тоже перпендикулярен оси цилиндрическогопроводника и сонаправлен e_φ орту в цилиндрической системекоординат. С учётом сонаправленности e_φ орта вектору dl обхода Г_м контура c внешнейстороны поперечного сечения цилиндрическогопроводникаH_l проекция наdl вектор равна H_φ проекции вектора H напряжённостимагнитного поляна e_φ орт, т.е. H_l= H_φ,и она является положительнойвеличиной при положительном направлении обхода Г_м контура R радиусом против "часовой стрелки" и направлении I макроскопического или тока проводимости по OZ оси.Поэтомус учётом равенстванулюпроекцийH _r, H _Z вектора H напряжённостимагнитного поляна соответственно e_r, e_Z орты в цилиндрической системекоординат эта H_l проекция равна H модулю (7.138) вектора H напряжённостимагнитного поляна Г_м контуре R радиусом.

где (рис.7. 32) r ≤ R; I - сила макроскопического или тока проводимости, текущего перпендикулярно поверхности S = πR² площадью, которая представляет собой поперечное сечение цилиндрического проводникаиз магнетика с χ_пр магнитной восприимчивостью, перпендикулярное его оси.

Вектор j_молплотности молекулярных токов внепроводящем магнетикес χ_м восприимчивостью, окружающемцилиндрическийпроводник с χ_пр магнитной восприимчивостью, по аналогии с (7.142) имеет с учётом (7.150) следующий вид:

j_мол = [J] = {(1/r)[∂(rJ_{м l})/∂r]}e_Z = (1/r)[∂(rχ_мI/2πr)/∂r]e_Z = (1/r)[∂(χ_мI/2π)/∂r]e_Z = 0,(7.151)

т.е. молекулярный токвнепроводящем магнетикеχ_м восприимчивостью, окружающемцилиндрическийпроводник с χ_пр магнитной восприимчивостью, отсутствует.

∫J_м dl= ∫J_{м |r =R} dl= J_{мl|r = R}2πR = (χ_м RI/2πR²)2πR = χ _мI А, (7.152) Г_м Г_{м |r = R}

где I - сила макроскопического или тока проводимости, текущего перпендикулярно поверхности S = πR² площадью, которая представляет собой поперечное сечение, перпендикулярное оси цилиндрического проводникаиз магнетикас χ_пр магнитной восприимчивостью; J_{мl|r = R} - проекция навектор dl обхода Г_м контура вектора J_мнамагниченности внепроводящем магнетике с χ _м магнитной восприимчивостью, который охватываетc внешнейстороны поперечное сечение цилиндрическогопроводника c χ_пр магнитной восприимчивостью, перпендикулярное его оси,вследствие чего длина этого Г_м контура r= R радиусом равна 2πR длине окружности.

Циркуляция (7.152) вектора J_м(r);намагниченностивнепроводящем магнетике с χ_м магнитной восприимчивостью повоображаемой окружности(рис.7.32) r= R радиусом Г_м контуру c внешнейстороны поперечного сечения цилиндрическогопроводникаиз магнетика c χ_пр магнитной восприимчивостью, перпендикулярного его оси (7.150), равна с учётом (7.152)следующей сумме охватываемых этим Г_м контуром:молекулярноготока I_мол = χ_прI силой(7.146), которыйтечёт через поперечное сечение, перпендикулярное осицилиндрическогопроводника c χ_пр магнитной восприимчивостью, R радиусомиS = πR² площадью, имолекулярного поверхностноготока_.I_{мол.пов.} силой,которыйтечёт по поверхностираздела цилиндрическогопроводника c χ_пр магнитной

∫J_{м|r =R} dl= I_мол + I_{мол.пов} ↔ I_{мол.пов} = ∫J_{м |r =R} dl - I_мол ↔ I_{мол.пов} = χ_мI - χ_прI = I(χ_м - χ_пр) А,(7.153) Г_{м |r = R} Г_{м |r = R}

Согласно(7.153)поверхностныйток_.I_{мол.пов.} силой,которыйтечёт по поверхностираздела цилиндрическогопроводника c χ_пр магнитной восприимчивостьюинепроводящего магнетика с χ_м магнитной восприимчивостью, окружающегоэтотцилиндрическийпроводник, направлен (рис.7.32) в одну сторону с макроскопическим или током проводимости(7.137) I силой, если χ_м - χ_пр>0. При χ_м - χ_пр<0 поверхностныйток_.I_{мол.пов.} силой течёт в противоположном направлении с макроскопическим или током проводимости I силой. При этом χ_м >0 и χ_пр >0 для парамагнетикови ферромагнетиков; χ_м < 0 и χ_пр <0 для диамагнетиков.

Согласно(7.153) молекулярныйрезультирующийток I_мол силой, текущий через поперечное сечение магнетика R радиусомS = πR² площадьюцилиндрическогопроводника, перпендикулярное его оси,определяется циркуляцией вектора J_пр(r)намагниченностиповоображаемой окружности(рис.7.32) r= R радиусом Г_пр контуру c внутреннейстороны поперечного сечения цилиндрическогопроводникаиз магнетика c χ_пр магнитной восприимчивостью и имеет следующий вид: I_мол = ∫J_прdl= ∫J_{пр|r =R} dl= J_{прl|r = R} 2πR,(7.154) Г_пр Г_{пр|r = R}

где J_{прl|r = R} - проекция навектор dl обхода Г_пр контура вектора J_прнамагниченности, который охватываетc внутреннейстороны поперечное сечение цилиндрическогопроводника c χ_пр магнитной восприимчивостью, перпендикулярное его оси,вследствие чего длина этого Г_пр контура r= R радиусом равна 2πR длине окружности.

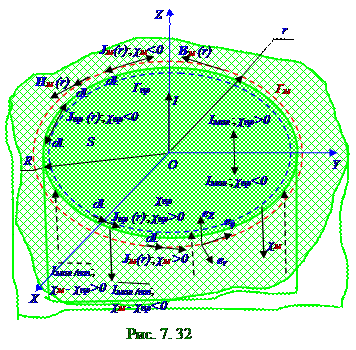
j_{мол.пов} плотности поверхностноготока_.,которыйтечётпо направлениюe_Z орта в цилиндрической системе координат, т.е. (рис.7.32) по направлению I макроскопического или тока проводимости, если разность J_{мl|r = R} проекции навектор dl обхода Г_м контура вектора J_мнамагниченности внепроводящем магнетике с χ_м магнитной восприимчивостью и J_{прl|r = R} проекции навектор dl обхода Г_пр контура вектора J_прнамагниченности вмагнетике с χ_пр магнитной восприимчивостью является положительнойвеличиной, т.е. если J_мl - J_прl > 0; если J_мl - J_прl < 0, то j_{мол.повZ} проекцияна e_Z орт в цилиндрической системе координат вектораj_{мол.пов} плотности поверхностноготока является отрицательнойвеличиной_.и поверхностныйток течётпротивоположно направлениюe_Z орта в цилиндрической системе координат, т.е. (рис.7.32) противоположно направлению I макроскопического или тока проводимости.

Модуль j_{мол.пов} вектораj_{мол.пов} плотности поверхностноготокаимеет размерность А/м и численно равен силе тока, протекающего (рис.7.32) перпендикулярно Г_пр, Г_м контурамчерез единицу длины этих контуров.

Модуль B(r) вектора B(r)индукции магнитного поля (7.127) в произвольной точке пространства, занятого магнетиком(рис.7.32)с μ_м магнитной проницаемостью, окружающегоцилиндрическийпроводник, в котором модуль H(r)вектора H(r)напряжённостимагнитного поля определяется (7.139), имеет следующий вид: B= μ₀ μ_мI_рез/2πr = μ_мB₀, (7.156)

где B₀ - модуль вектора B₀(r)индукции магнитного поля в вакууме(рис. 7. 31)с магнитнойμ_в проницаемостью, окружающегоцилиндрическийпроводник, равной единице, т.е. μ_в=1.

Физическая природа диамагнетизма

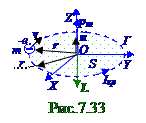
Вектор(7.77) из раздела 7.1 "Магнитостатика" магнитного p_mмомента плоскогоГ контурас круговымтоком I_кр силы, который создаёт -e электрон (рис.7.33), вращающийся по окружности r радиусом свектором vскорости вокруг ядра атома имеет следующий вид:

p_m = ISn ↔ p_m = IS = enπr² = e(v/2πr)πr² = evr/2,(7.157) гдеn - единичный вектор, нормальный к поверхности S площади круга,

скорости по окружности 2πr длиной; I = en - величина Δq заряда, переносимая через площадку в любом месте на пути движения электронаего e элементарнымзарядом запромежуток Δt времени, равный единице t времени, что делает возможным (6.3) из раздела 6.0 "Электрический ток"величину en считать круговымтоком I_кр силы; S = πr² - площадь круга, ограниченная окружностью, по которой двигается электрон; p_m - модуль вектора p_m магнитного момента, создаваемого вращающимся -e электроном, вследствие чего этот вектор p_m магнитного момента называют орбитальным магнитным моментом-e электрона.

Орбитальный p_m магнитный момент(рис.7.33) -e электрона образует с направлением вращения этогоэлектрона левовинтовую систему, а (1.68) из раздела 1.0 "Физические основы механики"векторL момента импульса-e электрона m массой относительно Oначалакоординат образует с направлением вращения этого-e электрона правовинтовую систему и имеет следующий вид: L =[r,mv], (7.158) где r ,v - соответственнорадиус - вектор и вектор скорости -e электрона. Поэтому вектор

L момент импульса, называемый орбитальным механическим моментом-e электрона, и

p_m орбитальный магнитный момент-e электронанаправлены (рис.7.33) в противоположные стороны.

Отношение проекций p_mz , L_z на OZ ось векторов орбитальныхсоответственно(7.157)

p_mмагнитного, (7.158) L механического моментов-e электрона называют магнитомеханическим или гиромагнитным отношением, которое имеет следующий вид: p_mz /L_z = (evr/2)/ -rmv = - e/2m, (7.159) где L_z = -rmv - проекция на OZ ось вектора (рис.7.33) орбитального(7.126) L механического момента -e электронаимеет знак "-",потому что этот вектор орбитального L механического момента -e электрона направлен противоположно OZ оси.

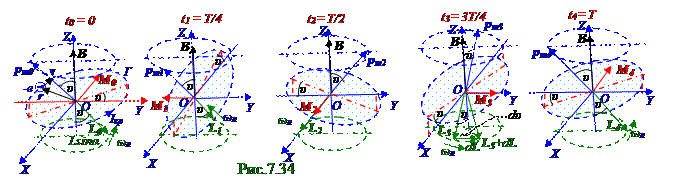
Вектор(7.82)из раздела 7.1 "Магнитное поле в вакууме. Движение заряженных частиц в электрическом и магнитном полях" M = [p_m, B] момента силы, действующего на контур с вектором p_mорбитального магнитного момента, который создаёт -e электрон (рис.7.33), вращающийся по окружности r радиусом свектором vскорости, направлен (рис.7.34) перпендикулярно плоскости, образованной этим вектором p_mмагнитного момента и вектором B индукциимагнитного поля в магнетике, вследствие чего модуль Mвектора M момента силы имеет следующий вид: M = p_mBsinυ,(7.160)

где υ - угол между векторами p_m и B; p_m, B - модули орбитальных векторов соответственно