Оценка однородности условий маркетинговой деятельности
Все этапы маркетинга как деятельности, направленной на удовлетворение нужд и потребностей людей, от производства товаров до потребления зависят от множества факторов, в том числе от неуправляемых и неконтролируемых. Результаты наблюдений характеризуются оценками математических ожиданий и дисперсий.
Если две (или несколько) выборки исследуемой величины получены при воздействии одних и тех же и с одинаковой интенсивностью влияющих на результат факторов (т. е. в однородных условиях), то оценки их математических ожиданий и дисперсий не должны существенно отличаться (т. е. выборки будут принадлежать одной и той же генеральной совокупности). Поэтому при проверке гипотезы об однородности двух выборок вначале проверяют однородность оценок дисперсий, позволяющую предположить однородность условий проведения наблюдений, и только в случае их однородности проверяют однородность средних.
Если при проведении эксперимента варьируется один (или несколько) из числа предположительно значимых факторов и при фиксации его (или их) на заранее выбранных уровнях, которые могут иметь место в естественных условиях, регистрируются значения исследуемой величины, то оценки дисперсий в выборках должны быть однородными, поскольку условия однородности воспроизведения опытов не нарушаются. Оценки математических ожиданий выборок будут неоднородными, если фактор (или несколько варьируемых факторов) значим, и однородными, если фактор незначим.
Во всех случаях однородность условий проведения опытов предполагает однородность оценок дисперсий. Обратное утверждение (однородность дисперсий означает однородность условий проведения опытов) может быть верным, если имеются все физические предпосылки для этого.
При сравнении двух выборочных независимых дисперсий используется F критерий Фишера, при этом для проверки нулевой гипотезы Н0: D*(x1) = D*(x2) вычисляется отношение большей оценки дисперсии к меньшей. В качестве конкурирующей принимается Н1: D*(x1) > D*(x2) либо Н2: D*(x1) ≠ D*(x2), во втором случае имеет место двусторонняя критическая область.
Найденное Fнабл. сравнивается с критическим значением (табл. 10 приложения) при заданном уровне значимости a
(a/2 при двусторонней критической области) и числах степеней свободы оценок дисперсий f1 и f2 (число степеней свободы оценки дисперсии равно объему наблюдений минус единица).
В случае Fнабл. < Fкр (a; f1; f2) гипотеза об однородности оценок дисперсий не отвергается.
Пример. В качестве сравнительной оценки культурного уровня населения, наличия культурных ценностей в стране существует показатель, характеризующий число посещений очагов культуры в течение года, приходящееся на 1 человека [19].
Для оценки однородности популярности различных центров культуры (табл. 9) требуется оценить однородность оценок дисперсий с помощью критерия Фишера (табл. 10 приложения).
Таблица 9
Уровень посещаемости музеев и театров за рубежом и в России на 1 января 1999 г.
| Страна | Посещение музеев, на 1 чел. в год | Посещение театров, на 1 чел. в год |
| Россия | 0,5 | 0,3 |
| США | 1,3 | 1,6 |
| Норвегия | 1,9 | 2,5 |
| Австрия | 1,8 | 2,0 |
| Канада | 1,7 | 2,1 |
| Германия | 1,2 | 1,6 |
| Италия | – | 1,4 |
| m*(x) | 1,4 | 1,6 |
| D*(x) | 0,27 | 0,49 |
Решение. Критерий Фишера F вычисляется по формуле

Следовательно, гипотеза об однородности оценок дисперсий не отвергается при уровне значимости α = 0,1. Сравнение средних, исключение резко выделяющихся наблюдений проводить можно. Кроме очевидного последнего места, занимаемого в настоящее время Россией можно предположить, что и музеи, и театры посещает публика одного уровня.
В тех случаях, когда требуется проверить гипотезу об однородности нескольких оценок дисперсий, вычисленных по выборкам одинакового объема, используют критерий Кокрена. Им удобно пользоваться, например, при проведении дисперсионного анализа.
Проверяется гипотеза Н0: D*1 (y) = D*2 (y) =…= D*n (y) при конкурирующей Н1: D*j (y) > D*1 (y) = D*2 (y) =…= D*i (y)=… = D*n (y).
G-статистика критерия Кокрена выражается формулой:
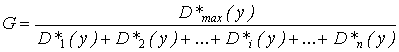 , (1.20)
, (1.20)
где D*max (y) = max(D*1 (y); D*2 (y);… D*i (y);… D*n (y)).
Если при уровне значимости α, числе степеней свободы каждой из оценок дисперсий f, равном объему каждой выборки минус единица, а также числе исследуемых оценок дисперсий n имеет место (табл. 11 приложения) выражение:
Gнабл.< Gкр.(α; f; n), (1.21)
то гипотеза об однородности оценок дисперсий не отвергается.
Пример 1. В табл. 10 приведены данные об объемах месячных продаж безалкогольного напитка «Тархун» в течение семи лет с 1993 по 1999 гг. [11]. Требуется оценить однородность оценок дисперсий ежемесячного потребления напитка, предполагающую неизменность воздействия значимых факторов на объем продаж по годам.
Таблица 10
Ежемесячное потребление безалкогольного напитка «Тархун» в 1993–1999 гг., тыс. дкл
| Месяц | Год | ||||||
| Январь | 6,7 | 7,2 | 7,7 | 7,9 | 8,4 | 8,5 | 8,8 |
| Февраль | 6,6 | 6,9 | 7,3 | 7,4 | 7,8 | 8,4 | 8,8 |
| Март | 8,5 | 9,1 | 8,7 | 8,9 | 10,2 | 10,6 | 11,2 |
| Апрель | 8,5 | 9,1 | 9,3 | 9,8 | 10,4 | 10,9 | 10,9 |
| Май | 9,1 | 10,0 | 10,2 | 10,1 | 11,2 | 11,0 | 11,9 |
| Июнь | 10,6 | 10,5 | 10,3 | 9,8 | 11,9 | 12,6 | 13,0 |
| Июль | 10,6 | 9,8 | 11,5 | 11,4 | 12,0 | 12,6 | 12,1 |
| Август | 10,5 | 10,4 | 11,0 | 11,9 | 11,1 | 12,0 | 12,8 |
| Сентябрь | 9,0 | 8,9 | 9,3 | 10,5 | 10,5 | 10,9 | 11,0 |
| Октябрь | 7,8 | 8,3 | 9,2 | 9,9 | 9,7 | 9,7 | 10,5 |
| Ноябрь | 7,9 | 8,1 | 8,3 | 8,9 | 9,8 | 9,6 | 9,8 |
| Декабрь | 8,1 | 8,3 | 8,3 | 9,3 | 9,6 | 9,7 | 9,4 |
| m*(y) | 8,7 | 8,9 | 9,3 | 9,7 | 10,2 | 10,5 | 10,9 |
| D*(y) | 1,91 | 1,38 | 1,68 | 1,68 | 1,62 | 2,01 | 2,09 |
Решение. В двух последних строках табл. 10 представлены оценки математических ожиданий и дисперсий. Значение
G-статистики

Следовательно, гипотеза об однородности оценок дисперсий не отвергается, что говорит о стабильности и однородности условий в течение семи лет, в которых осуществлялась продажа напитка. Постоянное ежегодное увеличение продаж напитка (m*(y) возрастает) свидетельствует об успешном внедрении маркетинговых мероприятий.
При оценке однородности нескольких оценок дисперсий, найденных по выборкам неодинакового объема (число выборок более трех) из нормально распределенных генеральных совокупностей, используют критерий Бартлетта, основанный на
М-статистике:
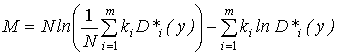 , (1.22)
, (1.22)
где 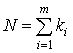 ; ki – число степеней свободы i-й дисперсии, равное соответствующему объему выборки минус единица; m – число сравниваемых оценок дисперсий; D*i(y) – оценка i-й дисперсии.
; ki – число степеней свободы i-й дисперсии, равное соответствующему объему выборки минус единица; m – число сравниваемых оценок дисперсий; D*i(y) – оценка i-й дисперсии.
Проверяется нулевая гипотеза Н0: D*1 (y) =…= D*i (y) = … = D*m (y) при конкурирующей Н1: D*1 (y) ≠ D*i (y). Табл. 12 приложения содержит критические значения М-статистики в зависимости от наперед заданного уровня значимости α, числа степеней свободы k = m – 1 и величин С1, С3, С,ΔС, вычисляемые по формулам
 (1.23)
(1.23)
В некоторых случаях используется функция m(α), вычисляемая по формуле,
 (1.24)
(1.24)
Правила, применяемые при использовании М-критерия [1]:
1. Вычисляется значение М-статистики (Мнабл.);
2. Мнабл. сравнивается со значениями ma и mb в строке k табл. 12 приложения; если при всех С1 величина ma ≤ M, то гипотезу о равенстве дисперсий Н0отвергают, если же при всех С1 имеет место М ≤ mb, то Н0не отвергается.
3. В тех случаях, когда max ma > M ≥ min mb, вычисляют С1 и по табл. 12, приложения находят ma(α; k; C1) и mb(α; k; C1); если ma(α; k; C1) ≤ M, то Н0 отвергается; если же М < mb(α; k; C1), то Н0 не отвергается.
4. При ma(α; k; C1) > M ≥ mb(α; k; C1) вычисляется значение m(α); если m(α) ≤ M, то Н0 отвергается; если же M < m(α), то Н0 не отвергается.
Пример 2. По данным табл. 11 проверить однородность оценок дисперсий экспорта продовольственных товаров и сырья для их производств, тыс. долл [17], из субъектов Российской федерации в 2000 г.
Таблица 11
Экспорт продовольственных товаров и сырья для их производства из субъектов Российской Федерации в 2000 г.
| № п/п | Субъект Российской Федерации | Экспорт (тыс. долл) |
| Субъекты РФ, экспортирующие максимум товаров | m*1 (y)= 151,7 | |
| Москва | 152,2 | |
| Камчатская область | 115,0 | |
| Ростовская область | 187,8 | |
| Северо-Западный федеральный округ | m*2 (y) = 34,9 | |
| Санкт-Петербург | 54,7 | |
| Калининградская область | 34,5 | |
| Мурманская область | 37,5 | |
| Новгородская область | 13,0 | |
| Южный федеральный округ и Самарская область | m*3 (y) = 31,6 | |
| Краснодарский край | 65,6 | |
| Ставропольский край | 23,0 | |
| Астраханская область | 16,2 | |
| Московская область | 57,6 | |
| Волгоградская область | 16,7 | |
| Самарская область | 26,9 | |
| Белгородская область | 15,4 | |
| Уральский и Сибирский федеральный округ | m*4 (y) = 31,7 | |
| Курганская область | 40,9 | |
| Челябинская область | 12,4 | |
| Алтайский край | 34,9 | |
| Новосибирская область | 17,0 | |
| Омская область | 53,3 | |
| Дальневосточный федеральный округ | m*5 (y) = 49,5 | |
| Приморский край | 81,2 | |
| Хабаровский край | 16,3 | |
| Сахалинская область | 51,1 |
Решение. Вычисляя по каждому j-му округу оценки математических ожиданий и дисперсий величин экспорта, их заносят в табл. 12.

Таблица 12
Вычисление параметров для нахождения М-статистики
| № п/п | D*i (y) | ki | 1/ki | kiD*i (y) | lnD*i (y) | kilnD*i (y) |
| 0,5 | 2650,4 | 7,1893 | 14,3786 | |||
| 292,9 | 0,33 | 878,6 | 5,6797 | 17,039 | ||
| 441,6 | 0,17 | 2649,7 | 6,0904 | 36,5425 | ||
| 287,5 | 0,25 | 1150,0 | 5,6612 | 22,6450 | ||
| 1054,8 | 0,5 | 2109,7 | 6,9611 | 13,9223 | ||
| Σ | 1,75 | 104,5274 |
М-статистика равна
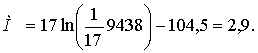
Так как при уровне значимости α = 0,05 и числе степеней свободы k =5 – 1 = 4 величина М-статистики mb(0,05; 4; C1) при любых C1 больше Мнабл. (по табл. 12 приложения минимальное значение mb(0,05; 4; 0,0) = 7,81), то гипотеза об однородности дисперсий не отвергается.
Замечание 1. Если предположить, что наблюдаемое значение М-статистики получилось равным 8,3, тогда необходимо было бы вычислить значение С1, оно было бы равно:

Используя линейную интерполяцию, по табл. 12 приложения получают mb(0,05; 4; 1,69) = 8,41. Поскольку оно превышает Мнабл., то и в этом случае гипотеза об однородности дисперсий не отвергалась бы.
2. Если предположить, что наблюдаемое значение М-статис-тики Мнабл. = 8,5, т. е. согласно табл. 12 приложения получится, что mb < Mнабл. < ma, то сначала нужно вычислить С3, С, ΔС:
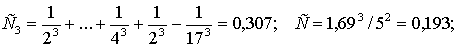
 .
.
Далее вычисляется величина m(α):

Поскольку предполагаемое Мнабл = 8,5 < m(α) = 9,01, то гипотеза об однородности дисперсий и в этом случае не отвергалась бы.
Дата добавления: 2016-03-27; просмотров: 635;
