Влияние квалификации специалистов на продолжительность технического обслуживания машин

Пример. Исследовать влияние квалификации специалистов, привлекаемых к проведению технических обслуживаний (ТО) машин, на продолжительность ТО. Специалисты разбиты на четыре группы (четыре уровня фактора А) в зависимости от их квалификации, оцениваемой стажем работы по специальности. В первую группу вошли слесари, имеющие стаж работы по специальности – не менее 8 лет, во вторую – не менее 12 лет, в третью – не менее 15 лет, в четвертую – не менее 20 лет. Из 20 автомобилей ЗИЛ-4314 (N = 20), имеющих приблизительно одинаковое техническое состояние, для каждого из специалистов случайным образом выбирается один и подается на таким же образом случайно выбранное рабочее место, причем все рабочие места имеют одинаковое техническое оснащение (эксперименты, поставленные в условиях, обеспечивающих случайный характер их проведения, называются рандомизированными). Результаты эксперимента приведены в табл. 14.

Таблица 14
Продолжительность проведения ТО по группам специалистов, мин

Решение. Для упрощения вычислений при ручном счете вычитается из всех данных 50 и формируется табл. 15.

Таблица 15
Расчетные значения параметров дисперсионного анализа

№ машины	Группа специалистов	Суммы
			–5	–8
			–4	–11
			–5	–5
			–11	–7
			–7	–9
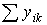
			–32	–40
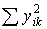
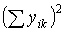
	8,3	13,7	7,8	5,0

Суммы ∑y_ik рассчитываются следующим образом: например, для второго столбца по первой группе специалистов 6 + 5 + +12 + 9 + 10 = 42.

Суммирование полученных значений по горизонтали дает следующий результат:

42 + 34 + (–32) + (–40) = 4.

Суммы 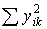рассчитываются так: например, для второго столбца по первой группе специалистов

6² + 5² + 12² + 9² + 10² = 386.

Суммирование полученных значений по горизонтали дает результат

386 + 286 + 236 + 340 = 1248,

который записывается в шестой столбец.

Суммы 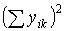получают, возводя в квадрат соответствующие суммы 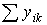по группам специалистов:

42² = 1764; 34² = 1156; (–32)² = 1024; (–40)² = 1600.

Суммируя вычисленные значения по горизонтали, получают сумму шестого столбца:

1764 + 1156 + 1024 + 1600 = 5544.

Проверяют однородность оценок дисперсий в соответствии с критерием Кокрена, вычисляют значение G-статистики:

G = 13,7/(8,3 + 13,7 +7,8 + 5,0) = 0,3940 < G_кр (0,05; 4; 4) = 0,6287.

Гипотеза об однородности оценок дисперсий не отвергается, предпосылки дисперсионного анализа не нарушаются, т. е. оценки внутригрупповой и общей дисперсии однородны.

Оценки суммарных квадратов, характеризующие общую дисперсию признака, дисперсию признака от воздействия фактора А, дисперсию признака от воздействия неучтенных факторов и ошибки эксперимента:

Q = 1248 – (4² / 20) = 1247,2; Q₁= (5544 / 5) – (4² / 20) = 1108;

Q₂ = 1248 – (5544 / 5) = 139,2.

Оценки дисперсий, соответствующие Q₁ и Q₂ при числах степеней свободы f₁= а – 1 = 4 – 1 = 3; f₂ = N – a = 20 – 4 = 16.

.

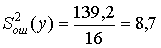Существенность фактора А проверяют с помощью F-критерия:

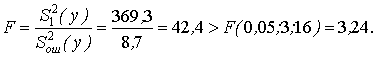
Значит, влияние квалификации на длительность ТО автомобилей существенно.

Чтобы количественно оценить вклад фактора А (квалификации специалистов) в изменчивость длительности ТО, находят оценки дисперсии вклада фактора А и полной дисперсии:

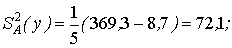
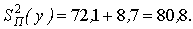
Вклад фактора А – квалификации специалистов в изменчивость продолжительности ТО

В_вкл = (72,1 / 80,8) 100 % = 89,3 %.

Следовательно, гипотеза о значимости влияния квалификации специалистов на продолжительность технических обслуживаний автомобилей ЗИЛ-4314 не отвергается и продолжительность проведения ТО при данных условиях оснащенности рабочих мест на 89,3 % определяется квалификацией специалистов.