Оценка существенности влияния двух факторов и их взаимодействия на показатели маркетинга
Модель двухфакторного дисперсионного анализа имеет вид
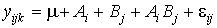 , (2.7)
, (2.7)
где уijk – значение признака у, когда фактор А находится на i-м уровне, фактор В – на j-м уровне при k-м повторении опыта; μ – среднее значение признака по результатам всех опытов; Аi – влияние на изменчивость признака фактора А, когда он находится на i-м уровне (эффект фактора А); Вj – эффект фактора В; АiВj – эффект взаимодействия факторов А и В, когда фактор А находится на i-м уровне, а фактор В – на j-м уровне; εijk – эффект ошибки эксперимента и действия неучтенных факторов.
В случае двухфакторного дисперсионного анализа полная дисперсия, обуславливающая изменчивость признака в серии опытов, дифференцируется на составляющие ее дисперсии, обусловленные варьированием независимых случайных переменных (факторов), ошибкой эксперимента и действием неучтенных факторов.
Пример 1. Оценить существенность влияния двух факторов (А – местонахождение пункта продаж автомобилей, В – время, месяц, год) на формирование цены подержанных легковых автомобилей. Данные приведены в табл. 16.
Решение. Вычисляют оценки математических ожиданий и дисперсий по группам наблюдений:
 (2.8)
(2.8)
Оценка математического ожидания признака – цены подержанного легкового автомобиля, когда факторы А и В находятся на первом уровне (первый уровень фактора А – местонахождение пункта продаж – Минск, первый уровень фактора В – ноябрь 2000 г.)

Оценка дисперсии 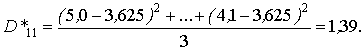
Оценка математического ожидания цены подержанного легкового автомобиля, когда местонахождение пункта продаж – Минск (первый уровень фактора А), а событие происходит в июле 2001 г. (второй уровень фактора В)
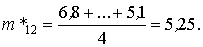
Оценка дисперсии цены 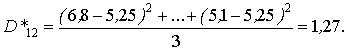
Оценка математического ожидания цены, когда местонахождения пункта продаж – Москва (второй уровень фактора А), а распродажа осуществлялась в ноябре 2000 г. (первый уровень фактора В)

Оценка дисперсии цены 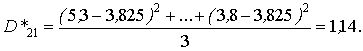
Оценка математического ожидания цены, когда факторы А и В находятся на втором уровне (пункт продажи – Москва, событие совершалось в июле 2001 г.)

Оценка дисперсии 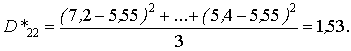
Проверка однородности оценок дисперсий осуществляется с помощью критерия Кокрена, вычисляется значение G-статистики:
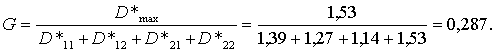
Поскольку при уровне значимости α = 0,05, четырех независимых оценках дисперсий (k = 4) и равных числах степеней свободы оценок дисперсий f = 3 критическое значение Gкр(0,05;4;3) = = 0,7814 > Gнабл.= 0,287 (табл. 11 приложения), то гипотеза об однородности оценок дисперсий не отвергается. Дисперсионный анализ можно проводить, так как с достаточно высоким уровнем доверительной вероятности можно предположить, что неучтенные факторы и ошибка эксперимента существенно не повлияли на цену подержанных легковых автомобилей ни в Минске, ни в Москве, ни осенью, ни летом.
Таблица 16
Влияние фактора А – местонахождения пункта продаж и фактора В – времени года на цены подержанных легковых автомобилей
| Уровень, сумма фактора В | Уровень фактора А | 
| 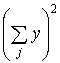
| 
| |
| 5,0 | 6,8 | ||||
| 3,1 | 4,1 | ||||
| 2,3 | 5,0 | ||||
| 4,1 | 5,1 | ||||
| Σ1у | 14,5 | 35,5 | 35,52 = 1260,25 | ||
| (Σ1у)2 | 210,25 | 170,77 | |||
| 5,3 | 7,2 | ||||
| 2,8 | 4,2 | ||||
| 3,4 | 5,4 | ||||
| 3,8 | 5,4 | ||||
| Σ2у | 15,3 | 22,2 | 37,5 | 37,52 = 1406,25 | |
| (Σ2у)2 | 234,09 | 492,84 | 189,73 | ||
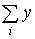
| 29,8 | 43,2 | 73,0 | ||
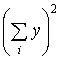
| 888,04 | 1866,24 | 2666,50 2754,28 | ||
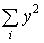
| 118,64 | 241,86 | 360,5 | ||
| m*11=3,625 D*11=1,39 | M*12= 5,25 D*12= 1,27 | ||||
| m*21=3,825 D*21=1,14 | M*22= 5,55 D*22= 1,53 |
Вычисление сумм, представленных в табл. 16, производилось следующим образом.
Суммы для первого уровня фактора В:
Σ11у = 5,0 + …+ 4,1 = 14,5; Σ12у = 6,8+ … + 5,1 = 21;
 ;
; 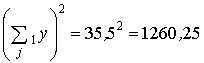 ;
;
(Σ11у)2 = 14,52 = 210,25; (Σ12у)2 = 212 = 441;
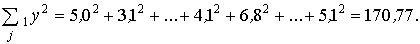
Суммы для второго уровня фактора В:
Σ21 у = 5,3 + … + 3,8 = 15,3; Σ22 у = 7,2 + …+ 5,4 = 22,2;
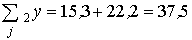 ;
;  ;
;
(Σ21 у)2 = 15,32 = 234,09; (Σ22 у)2 = 22,22 = 492,84;
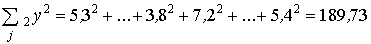 ;
; 
Далее рассчитаем суммы по уровням фактора А:
 ;
; 
Сделаем промежуточную проверку
 т. е. 29,8 + 43,2 = 35,5 + 37,5 = 73.
т. е. 29,8 + 43,2 = 35,5 + 37,5 = 73.
 ;
; 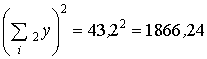 ;
; 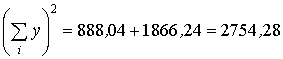 ;
; 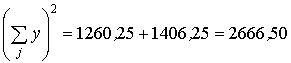 ;
; 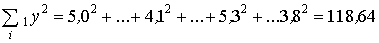 ;
;
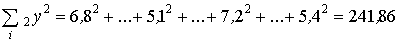 ;
;
 ;
; 
Последняя сумма дает проверку правильности вычислений, так как должно иметь место равенство

Считаем суммы, входящие в формулы для определения суммарных квадратов:
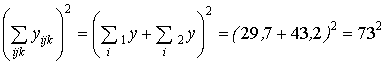 ;
; 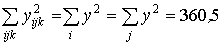 ;
;
 ;
;
 ;
;

Полный суммарный квадрат
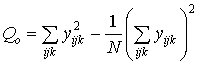 =
= 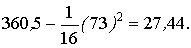
Суммарный квадрат, характеризующий эффект фактора В – времени года,
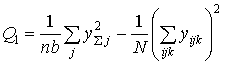 =
= 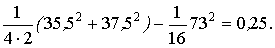
Суммарный квадрат, характеризующий эффект фактора А – местонахождения пункта продаж,
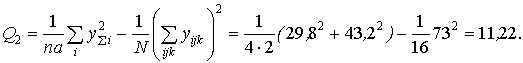
Суммарный квадрат эффекта взаимодействия
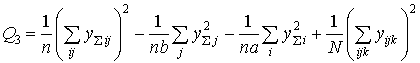 ;
;
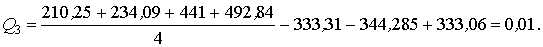
Суммарный квадрат, характеризующий ошибку эксперимента и действие неучтенных факторов,
 ;
;
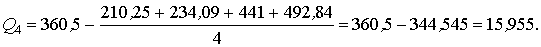
Оценки дисперсий, соответствующие суммарным квадратам,
 ; (2.9)
; (2.9)
где f – число степеней свободы дисперсии.
При общем числе наблюдений
N = abn = 2·2·4 = 16,
здесь а – число уровней фактора А, а = 2; b – число уровней фактора В, b = 2; n – число повторений опытов на каждом уровне, n = 4.
f0 = N – 1 = 16 – 1 = 15; f1= b – 1 = 2 – 1 = 1;
f2 = a – 1 = 2 – 1 = 1; f3 = (b – 1)(a – 1) = (2 – 1)(2 – 1) = 1;
f4 = ab(n – 1) = 2·2(4 – 1) = 12.
Оценки полной дисперсии и дисперсий, характеризующих изменчивость признака по всем наблюдениям,
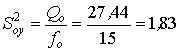 ;
; 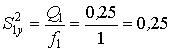 ;
;  ;
;
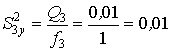 ;
; 
Существенность оценок дисперсий проверяют на фоне ошибки эксперимента и действия неучтенных факторов при нулевой гипотезе Н0: S2(y) > S24 (y) и конкурирующей Н1: S2 ≤ S24(y), используя критерий Фишера:
 ,
,
т. е. нуль-гипотезу отвергают при уровне значимости α = 0,05 и числах степеней свободы f1 = 1 и f4 = 12, принимается конкурирующая гипотеза (фактор времени года незначим).
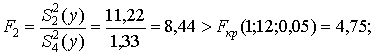
т. е. фактор местонахождения пункта продажи автомобилей существенно влияет на цену.

т. е. эффект взаимодействия факторов (местонахождения пункта продаж автомобилей и времени года) незначим.
Пример 2. Оценить наличие динамики роста продаж колбасных изделий (фактор А) за счет совершенствования этой сферы маркетинга и влияние разновидности колбасы (фактор В) на объем продаж (тыс. кг) в 2000 г. (табл. 17).
Уровни фактора А: 1. Январь, февраль, март; 2. Октябрь, ноябрь, декабрь; уровни фактора В: 1. Вареные колбасы; 2. Сардельки. Округленные данные взяты из источника [18].
Таблица 17
Исходные данные и расчет показателей для определения существенности факторов и их взаимодействий
| Уровень фактора В | Уровень фактора А | 
| 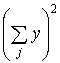
| 
| |
| 40,5 | 67,6 | ||||
| 40,2 | 67,3 | ||||
| 43,6 | 73,8 | ||||
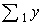
| 124,3 | 208,7 | |||

| 15450,5 | 43555,7 | 19702,7 | ||
| 5,6 | 10,0 | ||||
| 6,1 | 10,6 | ||||
| 7,0 | 10,1 | ||||

| 18,7 | 30,7 | 49,4 | 2440,4 | |
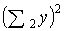
| 349,7 | 942,5 | 432,0 | ||
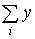
| 143,0 | 239,4 | 382,4 | ||
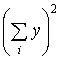
| 57312,4 | 113329,4 77761,4 | |||
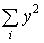
| 5274,8 | 14859,9 | 20134,7 |
Решение. Выполним проверку однородности оценок дисперсий по уровням факторов с помощью критерия Кокрена, для этого определим оценки параметров для соответствующих выборок по табл. 18.
Таблица 18
Параметры выборок по уровням факторов
| Параметр | A1B1 | A1B2 | A2B1 | A2B2 | Сумма |
| m*i (y) | 41,4 | 6,2 | 69,6 | 10,2 | – |
| D*i (y) | 3,54 | 0,503 | 13,46 | 0,103 | 17,61 |
Рассчитаем суммы для первого уровня фактора В:
Σ11y = 40,5 + 40,2 + 43,6 =124,3; Σ12y = 67,6 + 67,3 + 73,8 = 208,7;
(Σ11y)2 = 124,32 = 15450,5; (Σ12y)2 = 208,72 = 43555,7;
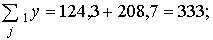
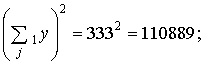

Рассчитаем суммы для второго уровня фактора В:
Σ21y = 5,6 + 6,1 + 7,0 = 18,7; Σ22y = 10,0 + 10,6 + 10,1 = 30,7;
(Σ21y)2 = 18,72 = 349,7; (Σ22y)2 = 30,72 = 942,5;
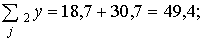


Рассчитаем суммы по уровням фактора А:

 ;
; 
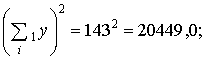

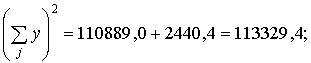

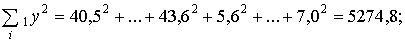
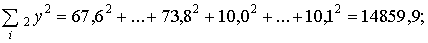


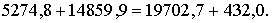
По формуле (1.20) вычисляем значение G-статистики:
Gнабл = 13,46 / (3,54 + 0,503 + 13,46 + 0,103) = 0,764 < Gкр (0,05; 4; 2) = 0,7679.
Поскольку оно меньше критического при уровне значимости α = 0,05, числе исследуемых оценок дисперсий, равном четырем, числах степеней свободы каждой из оценок дисперсий, равных двум, гипотеза об однородности оценок не отвергается [3, табл. 3.4 б]. Дисперсионный анализ можно проводить, поскольку существенного влияния на признак неучитываемые факторы не оказывали.
Рассчитаем суммы, входящие в формулы для определения суммарных квадратов:
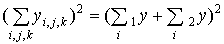 = (143,0 + 239,4)2 = 382,42 = 146229,8;
= (143,0 + 239,4)2 = 382,42 = 146229,8; 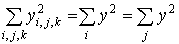 = 20134,7;
= 20134,7;  3332 + 49,42 =
3332 + 49,42 =
= 113329,4;  = 1432 + 239,42 = 77761,4;
= 1432 + 239,42 = 77761,4;
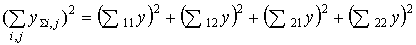 = 15450,5 + 43555,7 +
= 15450,5 + 43555,7 +
+ 349,7 + 942,5 = 60298,4;
Полные суммарные квадраты, характеризующие отклонение признака от общей средней, отклонение признака от воздействия фактора А – совершенствования системы маркетинга, отклонение признака от воздействия фактора В – разновидности колбасной продукции, изменчивость признака от взаимодействия факторов А и В, а также суммарный квадрат, характеризующий ошибку эксперимента и действие неучтенных факторов будут иметь следующие значения:
Q0 = 20134,7 – 146229,8 / 12 = 7948,9;
Q1 = (113329,4 / 3ּ2) – 146229,8 / 12 = 6702,4;
Q2 = (77761,4 / 3ּ2) – 146229,8 / 12 = 774,4;
Q3 = (60298,4 / 3) – (113329,4 / 3ּ2) – (77761,4 / 3ּ2) + (146229,8 / 12) = 436,9;
Q4 = 20134,7 – 60298,4 / 3 = 35,2.
Сделаем проверку: Q0 = Q1 + Q2 + Q3 + Q4.
7948,9 = 6702,4 + 774,4 + 436,9 + 35,2.
Числа степеней свободы оценок дисперсий имеют следующие значения:
f0 = N – 1 = 12 – 1 = 11; f1 = b – 1 = 2 – 1 = 1; f2 = a – 1 = 2 – 1 = 1;
f3 = (a –1)(b – 1) = (2 - 1)(2 – 1) = 1; f4 = ab(n – 1) = 2·2(3 – 1) = 8.
Оценки дисперсий соответственно полной, характеризующей отклонение признака от воздействия фактора А – совершенствования системы маркетинга; характеризующей отклонение признака от воздействия фактора В – разновидности колбасной продукции; характеризующей изменчивость признака от взаимодействия факторов А и В; характеризующей ошибку эксперимента и действие неучтенных факторов следующие:
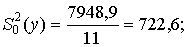
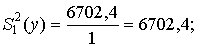

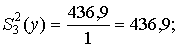

Проверим значимость оценок дисперсий с помощью критерия Фишера (табл. 10 приложения):

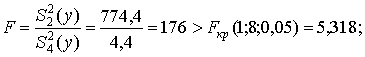
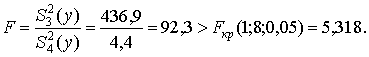
Оценим дисперсию роста продаж колбасных изделий в 2000 г. за счет динамичного развития этой сферы маркетинга по формуле
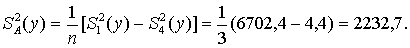
Оценим дисперсию, характеризующую влияние разновидности изделия на рост объема продаж:

Оценим дисперсию, характеризующую влияние эффекта взаимодействия факторов А и В (динамичного развития сферы маркетинга в части продаж колбасных изделий и разновидности изделий):
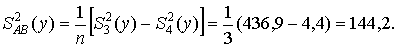
Оценим полную дисперсию изменчивости признака:
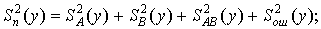
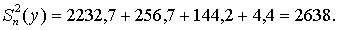
Оценим вклад фактора А в изменчивость признака:
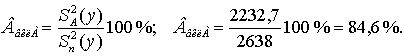
Оценим вклад фактора В в изменчивость признака:
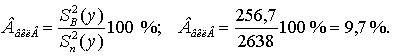
Оценим вклад эффекта взаимодействия в изменчивость признака:
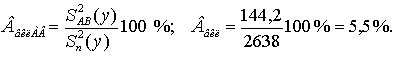
Оценим вклад ошибки эксперимента и действия неучтенных факторов в изменчивость признака:
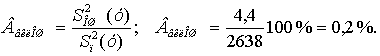
Таким образом, месячный объем продаж колбасных изделий в 2000 г. более чем на 84 % был обусловлен совершенствованием исследуемой сферы маркетинга в течение года, более чем на 9 % – приемлемым для покупателей ассортиментом, почти на 6 % – их взаимодействием при ошибке расчетов из-за неучтенных факторов и погрешностей эксперимента, составляющей менее одного процента.
Дата добавления: 2016-03-27; просмотров: 861;
