Термины, постановка задачи
Основной предмет изучения – связь между Q – количеством запаса на складе и временем, для которого рассматривается этот запас [20], т. е. исследуется функция Q = f(t). Затраты, связанные с запасами:
- Организационные издержки – расходы, обусловленные необходимостью оформления и доставки товара; они зависят также от подготовительно-заключительных операций при поступлении товара и подаче заявок и поэтому имеют место при каждом цикле складирования. Если запасы необходимо пополнить, то на склад завозится очередная партия. Издержки, связанные с поставкой, называются организационными. Количество товара, поставляемое на склад, называется размером партии.
- Издержки содержания запасов – это затраты, связанные с хранением (содержание или аренда помещений, естественная порча товара).
- Издержки, связанные с дефицитом (штрафы); если поставки со склада не могут быть выполнены, то возникают дополнительные издержки, обусловленные вынужденным отказом. Это может быть реальный денежный штраф, а может быть просто ухудшение бизнеса в будущем из-за потери разочаровавшихся в поставщике потребителей.
Основная модель управления запасами – определение оптимального размера партии.
В упрощенной модели рассматриваются следующие величины, представленные в табл. 34.
Таблица 34
Исходные данные для вычисления размера партии
| Параметр | Обозначение | Единица измерения | Условия эффективности применения модели |
| Интенсивность спроса | d | Единицы товара в год | Спрос постоянен и непрерывен, весь спрос удовлетворяется |
| Организационные издержки | s | У.е. за 1 партию | Организационные издержки постоянны и не зависят от размера партии |
| Стоимость товара | c | У.е. за единицу товара | Цена постоянна, рассматривается 1 вид товара |
Окончание табл. 34
| Издержки содержания запаса | h | У.е. за единицу товара в год | Стоимость хранения товара в течение года постоянна |
| Размер партии | q | Ед. товара в одной партии | Постоянная величина размера партии, поступление мгновенное, как только уровень запаса становится равным нулю |
Обычно задача управления запасами ставится так: определить размер партии q, при котором годовые затраты будут минимальны. Для условий задачи, сформулированных в табл. 34, зависимость Q = f(t) имеет вид, представляемый графиком (рис. 4.1).
|

Рис. 4.1. График изменения и пополнения запасов: Q – уровень запаса
(по оси ординат); q – размер поставки (начало цикла); F – площадь под
графиком; T – продолжительность цикла; q/2 – средний уровень запаса
Замечания: 1) чтобы удовлетворить годовой спрос d при размере поставки (партии) q нужно сделать d/q поставок в год;
2) средний уровень запасов q/2 = F/T; F – площадь под графиком за цикл Т.
Уравнение издержек:
С = С1(организационные издержки) + С2 (стоимость товара) + + С3 (общие издержки содержания запасов).
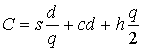 .
.
Оптимальное значение q находят, положив 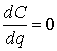 , т. е.
, т. е. 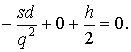
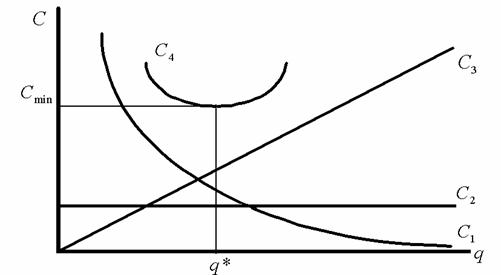
Рис. 4.2. График для определения оптимального размера партии:
С4 – суммарные издержки; Сmin – минимальные суммарные издержки;
q* – оптимальный размер партии
Решая уравнение относительно q – переменной величины, имеем
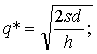
где q* – оптимальный размер партии.
Учитывая, что 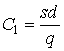 – общие организационные издержки, С2 = сd – стоимость товара, С3 =
– общие организационные издержки, С2 = сd – стоимость товара, С3 = 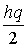 – общие издержки содержания запасов, получим график, приведенный на рис. 4.2.
– общие издержки содержания запасов, получим график, приведенный на рис. 4.2.
Дата добавления: 2016-03-27; просмотров: 627;
