БИБЛИОГРАФИЧЕСКИЙ СПИСОК 2 страница

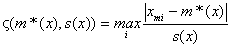
Число членов вариационного ряда n	Уровни значимости	Число членов вариационного ряда n	Уровни значимости
0,10	0,05	0,10	0,05
	1,412	1,414		2,764	2,929
	1,689	1,710		2,778	2,944
	1,869	1,917		2,792	2,958
	1,996	2,067		2,805	2,972
	2,093	2,182		2,818	2,985
	2,172	2,273		2,830	2,998
	2,238	2,349		2,842	3,010
	2,294	2,414		2,853	3,022
	2,343	2,470		2,864	3,033
	2,387	2,519		2,874	3,044
	2,426	2,563		2,885	3,055
	2,461	2,602		2,894	3,065
	2,494	2,638		2,904	3,075
	2,523	2,670		2,913	3,084
	2,551	2,701		2,922	3,094
	2,577	2,728		2,931	3,103
	2,601	2,754		2,940	3,112
	2,623	2,779		2,948	3,120
	2,644	2,801		2,956	3,129
	2,664	2,823		2,964	3,137
	2,683	2,843		2,972	3,145
	2,701	2,862		2,980	3,152
	2,718	2,880		2,987	3,160
	2,734	2,897		2,994	3,167
	2,749	2,913		3,001	3,175

Таблица 5
Критерии исключения резко выделяющихся наблюдений

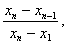
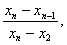
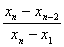
Число членов вариационного ряда n	Уровни значимости α	Число членов вариационного ряда n	Уровни значимости α
0,10	0,05	0,10	0,05
	0,886	0,941		0,332	0,392
	1,000	1,000		0,385	0,450
	1,000	1,000		0,449	0,504
Число членов вариационного ряда n	Уровни значимости α	Число членов вариационного ряда n	Уровни значимости α
0,10	0,05	0,10	0,05
	0,679	0,765		0,318	0,376
	0,910	0,955		0,367	0,428
	0,935	0,967		0,429	0,481
	0,557	0,642		0,285	0,338
	0,728	0,807		0,323	0,381
	0,782	0,845		0,382	0,430
	0,482	0,560		0,252	0,300
	0,609	0,689		0,282	0,334
	0,670	0,736		0,333	0,372
	0,434	0,507		0,234	0,281
	0,530	0,610		0,260	0,309
	0,596	0,661		0,309	0,347
	0,399	0,468		0,215	0,260
	0,479	0,554		0,236	0,283
	0,545	0,607		0,285	0,322
	0,370	0,437	–	–	–
	0,441	0,512	–	–	–
	0,505	0,565	–	–	–
	0,319	0,412	–	–	–
	0,409	0,477	–	–	–
	0,474	0,531	–	–	–

Таблица 6
Критерий Аббе

n	P = 0,05	n	P = 0,05	n	P = 0,05	n	P = 0,05
	0,3902		0,6417		0,7256		0,7698
	0,4103		0,6498		0,7292		0,7718
	0,4451		0,6574		0,7328		0,7739
	0,4680		0,6645		0,7363		0,7759
	0,4912		0,6713		0,7396		0,7779
	0,5121		0,6776		0,7429		0,7799
	0,5311		0,6836		0,7461		0,7817
	0,5482		0,6893		0,7491		0,7836
	0,5638		0,6946		0,7521		0,7853
	0,5778		0,6996		0,7550		0,7872
	0,5908		0,7046		0,7576		0,7891
	0,6027		0,7091		0,7603	∞	0,7906
	0,6137		0,7136		0,7628	–	–
	0,6237		0,7177		0,7653	–	–
	0,6330		0,7216		0,7676	–	–

Таблица 7
Критические точки распределения Стьюдента

Число степеней свободы k	Уровень значимости α(двусторонняя критическая область)
0,5	0,10	0,05
	1,0000	6,3138	12,7062
	0,8165	2,9200	4,3037
	0,7649	2,3534	3,1824
	0,7497	2,1318	2,7764
	0,7267	2,0150	2,5706
	0,7176	1,9432	2,4469
	0,7111	1,8946	2,3646
	0,7064	1,8595	2,3060
	0,7027	1,8331	2,2622
	0,6998	1,8125	2,2281
	0,6974	1,7959	2,2010
	0,6955	1,7823	2,1788
	0,6938	1,7709	2,1604
	0,6924	1,7613	2,1448
	0,6912	1,7530	2,1314
	0,6901	1,7459	2,1190
	0,6892	1,7396	2,1098
	0,6884	1,7341	2,1009
	0,6876	1,7291	2,0930
	0,6870	1,7247	2,0860
	0,6864	1,7207	2,0796
	0,6858	1,7171	2,0739
	0,6853	1,7139	2,0687
	0,6848	1,7109	2,0639
	0,6844	1,7081	2,0595
	0,6840	1,7056	2,0555
	0,6837	1,7033	2,0518
	0,6834	1,7011	2,0484
	0,6830	1,6991	2,0452
	0,6828	1,6973	2,0423
	0,6807	1,6839	2,0211
	0,6786	1,6706	2,0003
	0,6765	1,6577	1,9840
∞	0,6750	1,6479	1,9647
–	0,25	0,05	0,025
Уровень значимости α(односторонняя критическая область)

Таблица 8
Значения функции Лапласа

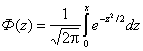
Х	Ф(x)	х	Ф(х)	Х	Ф(х)	х	Ф(х)
0,00	0,0000	0,38	0,1480	0,75	0,2734	1,12	0,3686
0,01	0,0040	0,39	0,1517	0,76	0,2764	1,13	0,3708
0,02	0,0080	0,40	0,1554	0,77	0,2794	1,14	0,3729
0,03	0,0120	0,41	0,1591	0,78	0,2823	1,15	0,3749
0,04	0,0160	0,42	0,1628	0,79	0,2852	1,16	0,3770
0,05	0,0199	0,43	0,1664	0,80	0,2881	1,17	0,3790
0,06	0,0239	0,44	0,1700	0,81	0,2910	1,18	0,3810
0,07	0,0279	0,45	0,1736	0,82	0,2939	1,20	0,3849
0,08	0,0319	0,46	0,1772	0,83	0,2967	1,21	0,3869
0,09	0,0359	0,47	0,1808	0,84	0,2995	1,22	0,3883
0,10	0,0398	0,48	0,1844	0,85	0,3023	1,23	0,3907
0,12	0,0478	0,49	0,1879	0,86	0,3051	1,24	0,3925
0,13	0,0517	0,50	0,1915	0,87	0,3078	1,25	0,3944
0,14	0,0557	0,51	0,1950	0,88	0,3106	1,26	0,3962
0,15	0,0596	0,52	0,1985	0,89	0,3133	1,27	0,3980
0,16	0,0636	0,53	0,2019	0,90	0,3159	1,28	0,3997
0,17	0,0675	0,54	0,2054	0,91	0,3186	1,29	0,4015
0,18	0,0714	0,55	0,2088	0,92	0,3212	1,30	0,4032
0,19	0,0753	0,56	0,2123	0,93	0,3238	1,31	0,4049
0,20	0,0793	0,57	0,2157	0,94	0,3264	1,32	0,4066
0,21	0,0832	0,58	0,2190	0,95	0,3289	1,33	0,4082
0,22	0,0871	0,59	0,2224	0,96	0,3315	1,34	0,4099
0,23	0,0910	0,60	0,2267	0,97	0,3340	1,35	0,4115
0,24	0,0948	0,61	0,2291	0,98	0,3365	1,36	0,4131
0,25	0,0987	0,62	0,2324	0,99	0,3389	1,37	0,4147
0,26	0,1026	0,63	0,2357	1,00	0,3413	1,38	0,4162
0,27	0,1064	0,64	0,2389	1,01	0,3438	1,39	0,4177
0,28	0,1103	0,65	0,2422	1,02	0,3461	1,40	0,4192
0,29	0,1141	0,66	0,2454	1,03	0,3485	1,41	0,4207
0,30	0,1179	0,67	0,2486	1,04	0,3508	1,42	0,4222
0,31	0,1217	0,68	0,2517	1,05	0,3531	1,43	0,4230
0,32	0,1255	0,69	0,2549	1,06	0,3554	1,44	0,4251
0,33	0,1293	0,70	0,2580	1,07	0,3577	1,45	0,4265
0,34	0,1331	0,71	0,2611	1,08	0,3599	1,46	0,4279
0,35	0,1368	0,72	0,2642	1,09	0,3621	1,47	0,4292
0,36	0,1406	0,73	0,2673	1,10	0,3643	1,48	0,4306
0,37	0,1443	0,74	0,2703	1,11	0,3665	1,49	0,4319
Х	Ф(х)	х	Ф(х)	х	Ф(х)	х	Ф(х)
1,50	0,4332	1,90	0,4713	2,30	0,4893	2,81	0,4975
1,51	0,4345	1,91	0,4719	2,31	0,4896	2,82	0,4976
1,52	0,4357	1,92	0,4726	2,32	0,4898	2,83	0,4977
1,53	0,4370	1,93	0,4732	2,33	0,4901	2,84	0,4978
1,54	0,4382	1,94	0,4738	2,34	0,4904	2,85	0,49781
1,55	0,4394	1,95	0,4744	2,35	0,4906	2,86	0,49782
1,56	0,4406	1,96	0,4750	2,36	0,4909	2,87	0,49795
1,57	0,4418	1,97	0,4756	2,37	0,4911	2,88	0,49801
1,58	0,4429	1,98	0,4761	2,38	0,4913	2,89	0,49807
1,59	0,4441	1,99	0,4767	2,39	0,4915	2,90	0,49813
1,60	0,4452	2,00	0,4772	2,40	0,4918	2,91	0,49819
1,61	0,4463	2,01	0,4773	2,41	0,4920	2,92	0,49820
1,62	0,4474	2,02	0,4783	2,42	0,4922	2,93	0,49830
1,63	0,4484	2,03	0,4788	2,43	0,4924	2,94	0,49840
1,64	0,4495	2,04	0,4793	2,44	0,4927	2,95	0,49841
1,65	0,4505	2,05	0,4798	2,45	0,4929	2,96	0,49846
1,66	0,4515	2,06	0,4803	2,46	0,4931	2,97	0,49851
1,67	0,4525	2,07	0,4808	2,47	0,4932	2,98	0,49860
1,68	0,4535	2,08	0,4812	2,48	0,4934	2,99	0,49861
1,69	0,4545	2,09	0,4817	2,49	0,4936	3,00	0,49865
1,70	0,4554	2,10	0,4821	2,50	0,4938	3,10	0,49903
1,71	0,4564	2,11	0,4826	2,51	0,4939	3,20	0,49931
1,72	0,4573	2,12	0,4830	2,52	0,4941	3,30	0,49951
1,73	0,4582	2,13	0,4834	2,53	0,4942	3,40	0,49966
1,74	0,4591	2,14	0,4838	2,54	0,4945	3,50	0,49976
1,75	0,4599	2,15	0,4843	2,55	0,4946	3,60	0,499841
1,76	0,4608	2,16	0,4846	2,60	0,4953	3,80	0,499928
1,77	0,4616	2,17	0,4850	2,67	0,4962	4,00	0,499968
1,78	0,4625	2,18	0,4854	2,68	0,4963	4,10	0,499979
1,79	0,4633	2,19	0,4858	2,69	0,4964	4,20	0,499987
1,80	0,4641	2,20	0,4861	2,70	0,4965	4,30	0,499991
1,81	0,4649	2,21	0,4864	2,71	0,4966	4,40	0,499995
1,82	0,4656	2,22	0,4868	2,72	0,4967	4,50	0,499997
1,83	0,4664	2,23	0,4872	2,73	0,4968	4,60	0,499997
1,84	0,4671	2,24	0,4875	2,74	0,4969	4,70	0,499997
1,85	0,4678	2,25	0,4878	2,75	0,4970	4,80	0,499997
1,86	0,4686	2,26	0,4881	2,76	0,4971	4,90	0,499997
1,87	0,4693	2,27	0,4884	2,77	0,4972	5,00	0,499997
1,88	0,4699	2,28	0,4887	2,78	0,4973	–	–
1,89	0,4706	2,29	0,4890	2,80	0,4974	–	–

Таблица 9
Критические точки распределения χ²

Число степеней свободы k	Уровень значимости α
0,20	0,10	0,05	0,025
	1,642	2,706	3,841	5,024
	3,219	4,605	5,991	7,378
	4,642	6,251	7,815	9,348
	5,989	7,779	9,488	11,143
	7,289	9,236	11,070	12,832
	8,558	10,645	12,592	14,449
	9,803	12,017	14,067	16,013
	11,030	13,362	15,507	17,535
	12,242	14,684	16,919	19,023
	13,442	15,987	18,307	20,483
	14,631	17,275	19,676	21,920
	15,812	18,549	21,026	23,336
	16,985	19,812	22,362	24,736
	18,151	21,064	23,685	26,129
	19,311	22,307	24,996	27,488
	20,465	23,542	26,296	28,845
	21,615	24,769	27,587	30,191
	22,766	25,989	28,869	31,536
	23,900	27,204	30,144	32,852
	25,038	28,412	31,410	34,170
	26,171	29,615	32,671	35,479
	27,301	30,813	33,924	36,781
	28,429	32,007	35,172	38,076
	29,553	33,196	36,415	39,364
	30,675	34,382	37,652	40,646
	31,795	35,563	38,885	41,923
	32,912	36,741	40,113	43,194
	34,027	37,916	41,337	44,461
	35,139	39,087	42,557	45,722
	36,250	40,256	43,773	46,979
	37,350	41,422	44,985	48,232
	38,466	42,585	46,194	49,480
	39,572	43,745	47,400	50,725
	40,676	44,903	48,602	51,966
	41,778	46,059	49,802	53,203
	42,879	47,212	50,998	54,437

Таблица 10
Критические точки распределения Фишера. Уровень значимости
α = 0,05 (k₁ – число степеней свободы большей дисперсии,
k₂ – число степеней свободы меньшей дисперсии)

<12 13 14 15 16 1718>

Дата добавления: 2016-03-27; просмотров: 419;