1 страница. Федеральное государственное образовательное бюджетное учреждение

ФЕДЕРАЛЬНОЕ АГЕНТСТВО СВЯЗИ

Федеральное государственное образовательное бюджетное учреждение

высшего профессионального образования

Московский технический университет связи и информатики

КАФЕДРА ЭЛЕКТРОНИКИ

Власов В.П., Каравашкина В.Н.

ФИЗИЧЕСКИЕ ОСНОВЫ ЭЛЕКТРОНИКИ

УЧЕБНОЕ ПОСОБИЕ

Москва 2015
CОДЕРЖАНИЕ

1. ОБЩАЯ ХАРАКТЕРИСТИКА ВЕЩЕСТВ В ЭЛЕКТРОНИКЕ

1.1. Электрические свойства веществ

1.2. Электрические заряды в полупроводниках

1.3. Энергетические диаграммы

1.4. Электропроводность полупроводников

1.5. Токи в полупроводниках

1.6. Особенности примесных полупроводников

1.7. Расчёт концентрации подвижных носителей заряда

2. ОБЩИЕ СВОЙСТВА КОНТАКТОВ ВЕЩЕСТВ В ЭЛЕКТРОНИКЕ

2.1. Контакты и структуры в электронике

2.2. Контактная разность потенциалов

2.3. Собственные токи в контактах

2.4. Электроёмкость контактов

2.5. Электрический и тепловой пробой в контактах.

3. КОНТАКТ МЕТАЛЛ – ПОЛУПРОВОДНИК. ДИОДЫ ШОТКИ

3.1. Основные свойства металло-полупроводниковых контактов

3.2. Диоды Шотки

4. КОНТАКТ ПОЛУПРОВОДНИКОВ Р- И N-ТИПА

4.1. Основные свойства p-n перехода

4.2. Основные числовые характеристики p-n перехода

4.3 Вольт-амперная характеристика p-n перехода

5. ДИОДЫ НА ОСНОВЕ M-N, P-N ПЕРЕХОДОВ И P-I-N СТРУКТУРЫ

5.1. Мощный выпрямительный диод

5.2. Импульсные и высокочастотные диоды

5.3. Стабилитрон

5.4. Варикап

5.5. Диоды на основе p-i-n структуры

5.6. Свето- и фото-диоды. Солнечные батареи

6. СТРУКТУРА МЕТАЛЛ-ДИЭЛЕКТРИК-ПОЛУПРОВОДНИК.

МДП- ТРАНЗИСТОР

6.1. Основные свойства МДП-структуры

6.2 МДП-транзистор с индуцированным каналом

6.3. Основные параметры МДП-транзистора

6.4. Статические характеристики МДП-транзистора

6.5. МДП-транзистор с плавающим затвором

6.6. Арсенид-галлиевый полевой транзистор

7. N-P-N И P-N-P СТРУКТУРЫ. БИПОЛЯРНЫЙ ТРАНЗИСТОР

7.1. Основные свойства биполярного транзистора

7.2. Биполярный транзистор в схеме с общей базой

7.3. Биполярный транзистор в схеме с общим эмиттером

7.4. Статические характеристики биполярного транзистора

8. ИНЕРЦИОННЫЕ СВОЙСТВА МДП И БИПОЛЯРНЫХ ТРАНЗИСТОРОВ

8.1. Причины инерционности МДП и биполярных транзисторов

8.2. Импульсные свойства МДП и биполярных транзисторов

8.3. Частотные свойства МДП и биполярных транзисторов

9. IGBT – ТРАНЗИСТОР

10. КОНТАКТ ПРОВОДНИК - ВАКУУМ. ЭЛЕКТРОННЫЕ ЛАМПЫ

11. КОМПЬЮТЕРНЫЕ МОДЕЛИ ЭЛЕКТРОННЫХ ЭЛЕМЕНТОВ

11.1. Компьютерная модель диода

11.2. Компьютерная модель транзистора

12. ШУМЫ ЭЛЕКТРОННЫХ ПРИБОРОВ

13. СПИСОК ЛИТЕРАТУРЫ

1. Общая характеристика веществ в электронике

1.1 Электрические свойства веществ. Полупроводники

Проводники содержат большое количество носителей заряда, способных перемещаться под действием электрического поля. Такие зарядыназывают подвижными, их направленное движение – электрическим током. Сила тока i определяется скоростью перемещения суммарного заряда подвижных носителей Q: i = dQ/dt. Способность вещества пропускать ток называется электропроводностью. Электропроводность определяется, главным образом, плотностью концентрации, или просто концентрацией подвижных носителей – их количеством в единице объёма. Типичными проводниками являются металлы. Для них характерна высокая концентрация подвижных зарядов – свободных электронов.

Диэлектрики практически не содержат подвижные заряды, их электропроводность ничтожна. Такими свойствами обладает большое число веществ.

Полупроводники занимают промежуточное положение по электропроводности межу проводниками и диэлектриками. Типичным и самым распространённым в электронике полупроводником является кремний (Si). Широкое применение находят также некоторые соединения, например арсенид галлия (GaAs).

Чистые, или собственные полупроводники содержат атомы только одного вида.Если в полупроводник при изготовлении намеренно введены примеси определённого вида в необходимой концентрации, то это примесный полупроводник. Полупроводники, как правило, используются в кристаллическом виде. В кристаллах атомы располагаются на строго определённых расстояниях друг от друга, в строго определённом взаимном расположении. Это гарантирует предсказуемость и повторяемость электрофизических свойств полупроводника, их однородность и следовательно, независимость от источника сырья, места, времени и условий изготовления.

Кристаллическая решётка кремния условно изображена на рис. 1. Кружки здесь – атомы кремния, двойные линии между кружками – связи между атомами. Такие связи возникают благодаря валентности – способности атомов соединяться и удерживаться на определённом расстоянии друг от друга. Валентные связи обеспечиваются парами валентных электронов – электронов внешней, валентной орбиты (оболочки), по одному от каждого из связанных атомов атома. Именно внешними оболочками «соприкасаются» атомы при сближении и именно валентные электроны образуют связи с соседними атомами. Согласно рис. 1 каждый атом кристаллического кремния обладает четырьмя валентными электронами и связан с четырьмя соседними атомами, т.е. валентность кремния равна 4.

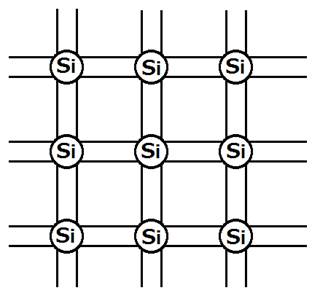
Рис. 1

На рис.1 кристаллическая решётка изображена в идеальном состоянии.

Однако в реальности полупроводник не может быть абсолютно чистым и бездефектным. От посторонних примесей и дефектов тщательно избавляются при изготовлении кристаллов для электронных элементов.

1.2 Электрические заряды в полупроводниках

Идеальное состояние решётки невозможно также при любой температуре, превышающей абсолютный нуль.При этом атомы и электроны хаотично колеблются относительно своих исходных положений, т.е. обладают некоторой тепловой энергией. Амплитуда и направление колебаний случайны и, вследствие обмена энергией при сближениях соседних атомов энергия хаотических тепловых колебаний электронов в некоторые моменты времени оказывается достаточной, чтобы они преодолели притяжение ядра и покинули атом. Такие электроны называются свободными или электронами проводимости, т.к. способны направленно двигаться под действием электрического поля. Свободными становятся, прежде всего, валентные электроны, наиболее удалённые от ядра и наименее с ним связанные.

На месте валентного электрона, ставшего свободным, образуется так называемая дырка – микрообласть с зарядом +q*, в которой отсутствует валентный электрон. Заряд появляется здесь вследствие нарушения равенства суммарного заряда электронов атома и заряда его ядра. Процесс образования свободного электрона и дырки, или электронно-дырочной пары, называется генерацией, рис. 2а. Если генерация обусловлена теплом, то это термогенерация. Генерация может вызываться и другими видами энергии, например, световой при освещении полупроводника.

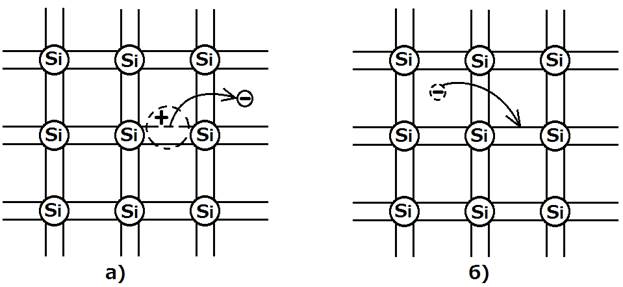
Рис. 2

Одновременно с генерацией происходит обратный процесс – рекомбинация. При этом перемещающийся по полупроводнику свободный электрон совпадает с дыркой, заполняет её и вновь становится валентным. Восстанавливается валентная связь и электрическая нейтральность данной микрообласти, свободный электрон и дырка исчезают, рис. 2б. В собственном полупроводнике генерация и рекомбинация свободных электронов и дырок происходит только парами, поэтому собственная концентрация свободных электронов n_i и собственная концентрация дырок p_i равны. Генерация происходит за счёт поглощения внешней энергии. Рекомбинация сопровождается её выделением, так как свободный электрон, превращаясь в валентный, теряет часть своей энергии. В частности, при рекомбинации полупроводник может светиться, что используется в светодиодах.

Дырка, как и свободный электрон, считается подвижным носителем заряда. При перемещении дырка заполняется не свободным, а соседним валентным электроном. Валентный электрон при этом остаётся валентным, его энергия не изменяется. Дырка исчезает на прежнем месте и возникает на новом месте, т.е. перемещается. Хотя при этом фактически перемещаются валентные электроны, воспринимается это, как перемещение единичного положительного заряда. Таким образом, перемещение зарядов в полупроводнике, т.е. возникновение тока, вызывается независимым друг от друга движением свободных электронов и дырок. Поэтому ток в полупроводниках может иметь как электронную I_n, так и дырочную I_p составляющие. Движение дырки поясняет рис. 3.

* q – элементарный, или единичный электрический заряд, равный …. Кл. Заряд электрона равен –q, дырки +q.

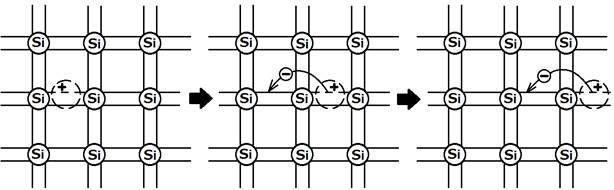
Рис. 3

Наряду с подвижными зарядами важную роль имеют неподвижные заряды – ионизированные атомы веществ, чаще всего примесей. Ионами называют атомы, утратившие часть своих электронов (положительные ионы) или захватившие посторонние электроны (отрицательные ионы). Ионы в твёрдых веществах не способны перемещаться и создавать ток. Однако, как и любые другие электрические заряды, они способны создавать электрическое поле, влияющее на подвижные заряды.

1.3 Энергетические диаграммы

Энергетическая диаграмма – график с главной осью y, на которой откладываются значения энергии W электронов вещества, обычно в электрон-вольтах, (эВ). Ось x позволяет отобразить изменение энергии вдоль главной координаты, в направлении движения носителей заряда. На рис. 4 изображена энергетическая диаграмма собственного полупроводника для образца с длиной l. Заштрихованные области соответствуют возможным значениям энергии электронов (разрешённые зоны). Просветы между ними – запрещённые зоны. Электронов с энергиями в пределах запрещённых зон в веществе нет.

Количество разрешённых и запрещенных зон в различных веществах различно.

В проводниках запрещённых зон нет вообще, в диэлектриках верхняя запрещённая зона очень широкая. Для полупроводников в электронике наиболее важны три верхних зоны (рис. 4). Самая верхняя из них, зона проводимости, соответствует энергиям свободных электронов. Под ней располагается запрещённая зона, электронов в которой нет*. Нижняя разрешённая зона – валентная зона, соответствует энергиям валентных электронов.

* Часто используемое выражение «электрон находится в зоне…» указывает не на место его расположения в пространстве, а на значение его энергии.

На энергетической диаграмме можно отобразить важные величины:

W_з – ширина запрещённой зоны;

W_c – дно зоны проводимости;

W_v – потолок валентной зоны.

Рис. 4

Энергетические диаграммы позволяют также графически отображать состояния и процессы в полупроводниках. Например, рис. 5 иллюстрирует генерацию и рекомбинацию в собственном полупроводнике.

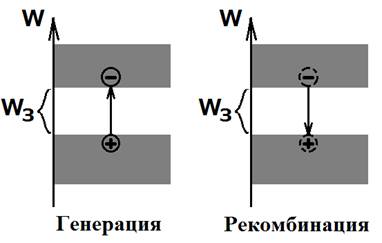
Рис. 5

Очевидно, что для превращения валентного электрона в свободный электрон необходима энергия не меньше

W_з = W_c - W_v (1)

Очевидно, что чем шире запрещённая зона полупроводника, тем слабее термогенерация и меньше собственная концентрация.

Такая же энергия выделяется при рекомбинации в виде тепла или света. Поэтому энергия кванта света hν при свечении полупроводника и, следовательно, цвет свечения определяются шириной запрещённой зоны:

hν = hc / λ = W_з, (2)

где h - постоянная Планка; ν, λ, c - частота, длина волны и скорость света.

Отсюда разнообразие полупроводников в светодиодах и в пикселах светодиодных экранов.

1.4 Электропроводность полупроводников

В физике полупроводников вместо понятий ток I и напряжение U удобнее пользоваться понятиями плотность тока J [А/м²] и напряжённость поля E [В/м]. В этом случае закон Ома имеет вид:

J = E/ρ (3) или J = σE, (4)

где ρ – удельное сопротивление [Ом/м], σ – удельная проводимость [См/м]. Очевидно, что электропроводность полупроводника тем больше, чем больше заряд свободных электронов и дырок -q и q, чем больше их концентрации n и p и чем быстрее они способны двигаться под действием электрического поля:

σ = q(µ_nn + µ_pp) (5)

Здесь µ_n и µ_p - коэффициенты подвижности свободных электронов и дырок – средние скорости их движения под действием электрического поля с напряжённостью 1 В/м.

Подстановка (5) в (4) даёт:

J = q(µ_nn + µ_pp)E (6)

Электронная и дырочная составляющие плотности тока складываются, так как противоположны и направления движения свободных электронов и дырок и знаки их зарядов.

Средняя скорость электронов (следовательно, и дырок) относительно невелика из-за столкновений электронов с атомами кристаллической решётки. При столкновениях часть кинетической энергии движущихся электронов передается атомам, чем вызывается выделение тепла в любой проводящей среде при протекании в ней тока.

Электропроводность собственного полупроводника быстро (экспоненциально) растёт с увеличением температуры, так как при этом усиливается термогенерация электронно-дырочных пар и растёт их концентрация.

1.5 Токи в полупроводниках

Дрейфовым током называется ток, обусловленный движением носителей заряда под действием электрического поля. Выражение (4) соответствует плотности дрейфового тока J_др. В общем случае дрейфовый ток может иметь электронную J_др.n и дырочную J_др.p составляющие.

Направленное движение носителей заряда может быть также результатом диффузии – повсеместно наблюдаемого физического явления. Диффузией называется движение любых подвижных частиц из области с большей в область с меньшей концентрацией, обусловленное их хаотическим тепловым движением. Если происходит диффузия заряженных частиц, наблюдается направленное перемещение зарядов, т.е. возникает диффузионный ток.

Диффузионный ток невозможен в однородной среде, концентрация подвижных зарядов в которой везде одинакова, а также при нулевой абсолютной температуре.

Плотности электронного и дырочного диффузионного токов, обусловленных диффузией свободных электронов и дырок, описываются выражениями:

J_дф.n = qD_n dn/dx (7), J_дф.p = - qD_p dp/dx (8)

Здесь D_n и D_p – коэффициенты диффузии свободных электронов и дырок; dn/dx и dp/dx – градиенты концентрации свободных электронов и дырок.

Коэффициенты диффузии, как и коэффициенты подвижности, характеризуют среднюю скорость движения свободных электронов и дырок. Она зависит от количества столкновений электронов с атомами кристаллической решётки, а также от температуры, поскольку с ростом температуры растет скорость хаотического теплового движения. Поэтому коэффициент диффузии пропорционален коэффициенту подвижности и температуре:

D = µkT/q, (9)

где k – постоянная Больцмана; T – абсолютная температура.

Градиент концентрации – это вектор, величина которого равна скорости увеличения или уменьшения концентрации. В общем случае он указывает направление наискорейшего увеличения концентрации или наискорейшего её уменьшения (антиградиент). В (7) и (8) используются одномерные градиенты, учитывающие изменение концентрации в главном направлении x.

На рис. 6 изображен образец полупроводника, в левой части p⁺ которого концентрация дырок больше, чем в правой части р. Ниже построены зависимости концентрации и градиента концентрации дырок от координаты x. Очевидно, что в переходной области будет происходить диффузия дырок слева направо. В глубине областей, где полупроводник однороден, диффузии не будет.

Положительным направлением тока считается направление движения положительных зарядов (или обратное направление, если заряды отрицательные). Именно так движутся дырки в образце, вдоль положительного направления x. Согласно (8), отрицательный градиент образца дал бы отрицательное значение плотности тока и тока, если бы это выражение не имело знак «минус».

1.6 Особенности примесных полупроводников

В собственных полупроводниках концентрации свободных электронов и дырок равны (собственная концентрация n_i). Однако для электронных элементов и интегральных схем необходимы полупроводники с преобладанием свободных электронов (n – тип) и с преобладанием дырок (р – тип). Их называют также полупроводниками с электронной и дырочной проводимостью.

Чтобы получить полупроводник n – типа, в него при изготовлении кристалла добавляют донорную примесь. Атомы такой примеси имеют большую, чем сам полупроводник, валентность. Например, в кремний (число валентных электронов на внешней электронной оболочке равно 4) может быть добавлен фосфор (валентность 5). Это означает, что в полупроводнике появятся избыточные электроны, не участвующие в образовании связей между атомами. Такие электроны легко становятся свободными, достигается преобладание свободных электронов. Преобладающие по количеству носители называются основными. Неосновных носителей обычно на несколько порядков меньше.

На рис. 7 изображена энергетическая диаграмма полупроводника n – типа. Донорная примесь порождает разрешённые уровни в запрещённой зоне, вблизи дна зоны проводимости.

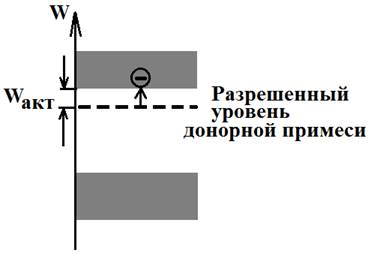
Рис. 7

Электроны с таким уровнем энергии становятся свободными при приобретении очень небольшой дополнительной энергии, энергии активации W_акт. Поэтому активация примеси происходит уже при низких температурах, когда термогенерация подвижных носителей самим полупроводником незначительна. Зависимость концентрации свободных электронов n от температуры Т приобретает вид рис. 8.

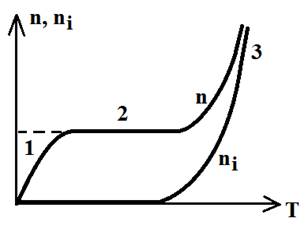
Рис. 8

Участок 1 этой зависимости соответствует быстрому росту концентрации за счет активации примеси. Рост прекращается, когда будут активированы все атомы примеси (участок 2). В области высоких температур рост возобновляется за счёт усиления термогенерации атомами самого полупроводника (участок 3).

На этом же рисунке показана экспоненциальная зависимость концентрацииn_i для собственного полупроводника. По сравнению с ним примесный полупроводник обладает большим достоинством – наличием обширного участка 2 с практически неизменной концентрацией и проводимостью в большом диапазоне температур T₁ – T₂. Выбирая концентрацию донорной примеси N_д при изготовлении можно получать желательные и стабильные параметры полупроводника в необходимом диапазоне температур. При этом обеспечивается соотношение:

n = N_д + n_i ≈ N_д = const (10)

Аналогичные изменения происходят при добавлении акцепторной примеси для изготовления полупроводника р – типа. Такая примесь, например бор с валентностью 3, имеет меньшую, чем кремний, валентность, что приводит к дефициту валентных электронов. Достигается преобладание дырок. Появление акцепторных атомов приводит к появлению разрешённых уровней в запрещённой зоне вблизи потолка валентной зоны, рис. 9.

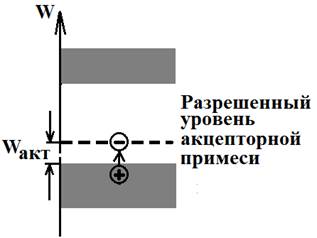
Рис. 9

Эти уровни легко заполняются валентными электронами, для чего требуется небольшая дополнительная энергия активации W_акт. Температурная зависимость концентрации дырок такая же, как и у полупроводника n – типа. На термостабильном участке выполняется аналогичное (10) соотношение:

p = N_а + n_i ≈ N_а = const, (11)

где N_а – концентрация акцепторной примеси.

На рис. 10 изображены фрагменты кристаллических решёток с донорным (рис. 10а) и акцепторным (рис. 10б) атомом.

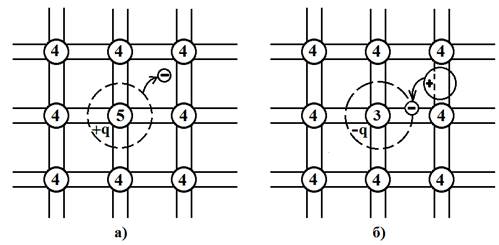
Рис. 10

При утрате одного из пяти валентных электронов донорного атома он превращается в положительно заряженный ион. Суммарный заряд этого иона и порождённого донорным атомом свободного электрона равен нулю, полупроводник остаётся электрически нейтральным. Однако, если свободный электрон исчезнет, например в результате рекомбинации, заряд иона становится «заметным», электрическая нейтральность нарушается. Такие ионы называются нескомпенсированными ионами донорной примеси. Каждый такой ион, как и дырка, имеет заряд +q, однако в отличие от дырки является неподвижным зарядом. Чем больше таких ионов, тем сильнее создаваемое ими электрическое поле, которое влияет на процессы в полупроводнике.

Аналогично, при захвате акцепторным атомом недостающего валентного электрона, он превращается в отрицательно заряженный ион. Возникшая при этом дырка уравновешивает заряд иона, однако, если дырка исчезает из окрестности иона, ион становится нескомпенсированным ионом акцепторной примеси с зарядом –q. Суммарное электрическое поле таких ионов также влияет на процессы в полупроводнике.

1.7 Расчёт концентрации подвижных носителей заряда

Для определения собственной концентрации заданного полупроводника при заданной температуре можно воспользоваться формулой:

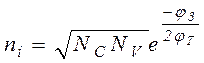(12)

В неё входит ряд констант, определённых для используемых в электронике полупроводников с высокой точностью и приводимых как в научной, так и в учебной литературе. Кроме того, в литературе часто указываются значения n_i

для основных полупроводников при комнатной температуре Т_комн . При такой температуре для кремния n_i ≈ 10¹⁰ см^-3 . Обращает на себя внимание ничтожность этой величины по сравнению с концентрацией атомов самого полупроводника N_ат ≈ 10²³ см^-3 . Если известна концентрация примеси, например, донорной примеси N_д и полупроводник используется в диапазоне температур, обеспечивающем стабильность параметров, для определения концентрации основных носителей можно воспользоваться формулой (10). При типичной для полупроводниковых элементов концентрации примесей 10¹⁸ см^-3 концентрация основных носителей n будет такой же.

Концентрацию неосновных носителей р можно найти из соотношения:

np = n_i² (13)

Это соотношение отражает очевидный факт: если температура неизменна (n_i = const), то чем больше основных носителей, тем меньше неосновных, так как с ростом концентрации основных носителей возрастает вероятность их встречи с неосновными носителями и их рекомбинации.

Для рассматриваемого примера для кремния при комнатной температуре из (13) следует:

p = n_i²/n= 10² см^-3

Обращает на себя внимание ничтожность концентрации неосновных носителей 10² см^-3 по отношению к концентрации основных носителей 10¹⁸ см^-3. Тем не менее, неосновные носители часто являются главными факторами процессов в электронных элементах и интегральных схемах.

2. ОБЩИЕ СВОЙСТВА КОНТАКТОВ ВЕЩЕСТВ В ЭЛЕКТРОНИКЕ

2.1 Контакты и структуры в электронике

В электронике используются самые различные вещества – проводники, полупроводники, диэлектрики. Они образуют самые разнообразные контакты, в которых наблюдаются контактные явления. Многослойные контакты называют структурами. Примерами контактов являются контакты металлов, призванные беспрепятственно пропускать ток, контакт полупроводников p и n-типа (p-n переход). Примерами структур являются электрический конденсатор, в котором контактируют металл, диэлектрик и снова металл (структура МДМ), МДП-структура, в которой контактируют металл, диэлектрик и полупроводник. МДП-структура является основой самого распространённого электронного элемента нашего времени – МДП-транзистора.

2.2 Контактная разность потенциалов

На границе упомянутых веществ всегда возникает электрическое поле, сила которого характеризуется напряжённостью поля Е или, чаще, контактной разностью потенциалов φ_к.

На рис. 11 изображён контакт двух металлов.

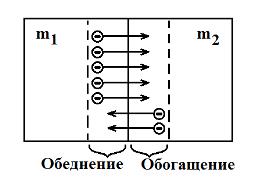
Рис. 11

Концентрация свободных электронов в металлах очень высокая. При ненулевой температуре они хаотично движутся, обладая в отдельные моменты времени большой кинетической энергией. Если эта энергия достаточна для выхода электрона из металла, он пересекает контакт и переходит в смежную область. Таким образом, наблюдаются два встречных потока электронов. Если металлы неодинаковы, неодинакова и сила этих потоков. В результате в одной из приграничных областей концентрация свободных электронов увеличится (обогащение), в другой – уменьшится (обеднение). Равенство по модулю положительных зарядов ядер и отрицательных зарядов электронов в этих областях нарушается, они приобретают заряд: отрицательный в обогащенной области, положительный в обеднённой области. Эти заряды создают в приграничных областях электрическое поле с контактной разностью потенциалов φ_к.

Работа, которую надо совершить, для выхода электрона из металла, называется работой выхода. Численно она равна qφ, где φ – потенциал электрического поля на поверхности. Для металлов с работами выхода qφ₁ и qφ₂ контактная разность потенциалов определяется выражением:

φ_к = φ₁ - φ₂ (14)

Контактная разность потенциалов возникает на границе любых типов проводников и полупроводников. Причиной этого, как и в случае двух металлов, является нарушение электрической нейтральности приграничных областей из-за перемещения зарядов.

Электрическое поле в контакте может способствовать или препятствовать движению подвижных носителей заряда. Потому распространён термин потенциальный барьер, высота которого равна φ_к.

Хотя для контактов между металлами характерна небольшая величина φ_к и они хорошо проводят ток, некоторые пары металлов как электрические контакты недопустимы. Так, контакт алюминиевого и медного проводов нарушается и даже разрушается в течение короткого времени. Причина – электрохимическая коррозия, обусловленная наличием φ_к .

2.3 Собственные токи в контактах

Так как проводники и полупроводники способны проводить ток, в контактах между ними в отсутствие внешнего напряжения могут возникать токи.

Рассмотрим, например, контакт полупроводников, отличающихся только концентрацией донорной примеси, рис. 12.

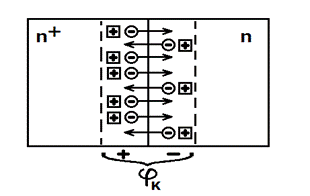
Рис. 12

Здесь левая область, обозначенная как n⁺, обладает более высокой концентрацией примесей и основных носителей – свободных электронов. В таком контакте существуют условия для возникновения диффузии: концентрация свободных электронов в n⁺ области больше, чем в n области, температура не равна нулю. Свободные электроны будут диффундировать из n⁺ области в n область (обозначены на рисунке кружками, стрелка указывает направление движения). Следовательно, в таком контакте существует диффузионный ток I_дф.